题目内容
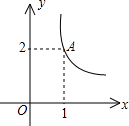 如图,l1是反比例函数y=
如图,l1是反比例函数y=| k |
| x |
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
分析:因为l1关于x轴对称的图象为l2,因此可知道A关于x轴的对称点A′在l2的函数图象上,从而可求出解析式.
解答:解:A(1,2)关于x轴的对称点为(1,-2).
所以l2的解析式为:y=-
,
因为l1是反比例函数y=
在第一象限内的图象,
所以x>0.
故选D.
所以l2的解析式为:y=-
| 2 |
| x |
因为l1是反比例函数y=
| k |
| x |
所以x>0.
故选D.
点评:本题考查反比例函数的性质,知道一点可以确定函数式,因此根据对称找到反比例函数上的点,从而求出解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
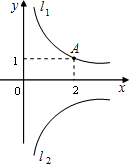 如图,l1是反比例函数y=
如图,l1是反比例函数y=| k |
| x |
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
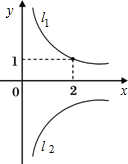 如图,l1是反比例函数
如图,l1是反比例函数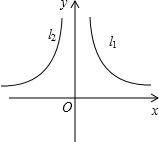 如图,l1是反比例函数y=
如图,l1是反比例函数y=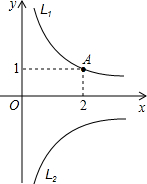 如图,L1是反比例函数y=
如图,L1是反比例函数y=