题目内容
 如图,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断a∥b的条件共有种.
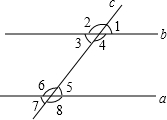
如图,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断a∥b的条件共有种.
- A.1种
- B.2种
- C.3种
- D.4种
B
分析:在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答:①若∠2=∠6,则根据“同位角相等,两直线平行”可以判定a∥b.故①正确;
②若∠2=∠8时,则∠4=∠8,所以根据“同位角相等,两直线平行”可以判定a∥b.故②正确;
③∠1与∠4互为邻补角,所以根据∠1+∠4=180°不能判定a∥b.故③错误;
④若∠3=∠8时,则∠3=∠6,根据“同旁内角相等”不能判定a∥b.故④错误;
综上所述,正确的说法有2个.
故选B.
点评:本题考查了平行线的判定.正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
分析:在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
解答:①若∠2=∠6,则根据“同位角相等,两直线平行”可以判定a∥b.故①正确;
②若∠2=∠8时,则∠4=∠8,所以根据“同位角相等,两直线平行”可以判定a∥b.故②正确;
③∠1与∠4互为邻补角,所以根据∠1+∠4=180°不能判定a∥b.故③错误;
④若∠3=∠8时,则∠3=∠6,根据“同旁内角相等”不能判定a∥b.故④错误;
综上所述,正确的说法有2个.
故选B.
点评:本题考查了平行线的判定.正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
相关题目
 如图,是一个挂在墙壁上时钟的示意图.O是其秒针的转动中心,M是秒针的另一端,OM=8cm,l是过点O的铅直直线.现有一只蚂蚁P在秒针OM上爬行,蚂蚁P到点O的距离与M到l的距离始终相等.则1分钟的时间内,蚂蚁P被秒针OM携带的过程中移动的路程(非蚂蚁在秒针上爬行的路程)是
如图,是一个挂在墙壁上时钟的示意图.O是其秒针的转动中心,M是秒针的另一端,OM=8cm,l是过点O的铅直直线.现有一只蚂蚁P在秒针OM上爬行,蚂蚁P到点O的距离与M到l的距离始终相等.则1分钟的时间内,蚂蚁P被秒针OM携带的过程中移动的路程(非蚂蚁在秒针上爬行的路程)是
 什么?
什么? 什么?
什么?
