题目内容
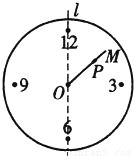
如图，是一个挂在墙壁上时钟的示意图．O是其秒针的转动中心，M是秒针的另一端，OM=8cm，l是过点O的铅直直线．现有一只蚂蚁P在秒针OM上爬行，蚂蚁P到点O的距离与M到l的距离始终相等．则1分钟的时间内，蚂蚁P被秒针OM携带的过程中移动的路程（非蚂蚁在秒针上爬行的路程）是
16π
16π
cm．分析：做出辅助线得出△OMN∽△Q 2OP，进而得出∠OPQ 2=∠NOM=90°，得出从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2在直径的两个圆，求出即可．
解答：解：过M作MN⊥L于点N，过O作L的垂线交于点Q 1，Q 2，连接PQ 1，则MN∥OQ 2，
∠M=∠MOQ 2，
∵OM=OQ 2，MN=OP，
∴△OMN∽△Q 2OP，
∴∠OPQ 2=∠NOM=90°，
∴点P在以OQ1为直径的圆上，同理点P在以OQ 2为直径的圆上，
从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2在直径的两个圆，移动的路程为：
2×8π=16π．
故答案为：16π．
∠M=∠MOQ 2，
∵OM=OQ 2，MN=OP，
∴△OMN∽△Q 2OP，
∴∠OPQ 2=∠NOM=90°，
∴点P在以OQ1为直径的圆上，同理点P在以OQ 2为直径的圆上，
从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2在直径的两个圆，移动的路程为：
2×8π=16π．
故答案为：16π．
点评：此题主要考查了弧长的计算以及物体移动路线问题，此题综合性较强得出从而蚂蚁P在1分钟时间内被秒针OM携带的过程中移动的轨迹就是分别以OQ1，OQ2在直径的两个圆是解决问题的关键．
练习册系列答案
相关题目
