题目内容
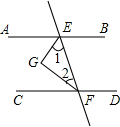
如图，已知直AB、CD被直线EF所截，GE平分∠AEF，GF平分∠EFC，∠1+∠2=90°，AB∥CD吗？为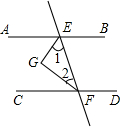
什么？
解：因为GE平分∠AEF，GF平分∠EFC（已知），
所以∠AEF=2∠
∠EFC=2∠
所以∠AEF+∠EFC=
因为∠1+∠2=90°（已知），
所以∠AEF+∠EFC=
所以AB∥CD
什么？解：因为GE平分∠AEF，GF平分∠EFC（已知），
所以∠AEF=2∠
1
1
，∠EFC=2∠
2
2
，所以∠AEF+∠EFC=
2（∠1+∠2）（
2（∠1+∠2）（
（ 等式性质 ），因为∠1+∠2=90°（已知），
所以∠AEF+∠EFC=
180°
180°
°所以AB∥CD
同旁内角互补，两直线平行
同旁内角互补，两直线平行
．分析：利用平行线的判定方法中的“同旁内角互补，两直线平行”即可得到结论．
解答：解：因为GE平分∠AEF，GF平分∠EFC（已知），
所以∠AEF=2∠1，
∠EFC=2∠2，
所以∠AEF+∠EFC=2（∠1+∠2）（ 等式性质 ），
因为∠1+∠2=90°（已知），
所以∠AEF+∠EFC=180°
所以AB∥CD（同旁内角互补，两直线平行）．
故答案为：1、2、2（∠1+∠2）、180°、同旁内角互补，两直线平行．
所以∠AEF=2∠1，
∠EFC=2∠2，
所以∠AEF+∠EFC=2（∠1+∠2）（ 等式性质 ），
因为∠1+∠2=90°（已知），
所以∠AEF+∠EFC=180°
所以AB∥CD（同旁内角互补，两直线平行）．
故答案为：1、2、2（∠1+∠2）、180°、同旁内角互补，两直线平行．
点评：本题考查了平行线的判定，牢记平行线的三个判定定理是解决此类题目的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=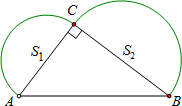
（2012•咸丰县二模）如图，已知在Rt△ABC中，∠ACB=90°，AB=10，分别以AC、BC为直经作半圆，面积分别记为S1、S2，则S1+S2的值等于（ ）
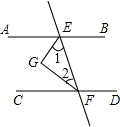什么？