题目内容
【题目】如图①,在正方形ABCD中,E是线段AB上一动点,点F在AD的延长线上运动,且DF=BE.
(1)求证:CE=CF.
(2)当点E在AB上运动时,在AD上取一点G,使∠GCE=45°,试判断BE、EG、GD三条线段的数量关系,并加以证明.
(3)若连接图①中的BD,分别交CE、CG于点M、N,得图②,试根据(2)中的结论说明以线段BM、MN、DN为三边构成的是一个什么形状的三角形?
【答案】
(1)
解:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF,
∴CE=CF
(2)
解:EG=BE+GD
理由:由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°,
又∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG,
∴GE=GF
∴GE=GF=DF+GD=BE+GD
(3)
解:如图,
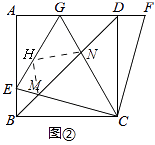
在GE上取一点H,使GH=GD,
∵△GCE≌△GCF,
∴∠DGN=∠HGN,∠F=∠GEC,
∵GN=GN,
∴△DGN≌△HGN,
∴DN=HN,
∴∠GDN=∠GHN=45°,
∵GE=GF,GD=GH,BE=DF,
∴DF=BE=EH,
∵∠F=∠GEC=∠BEC,∠EM=EM,
∴△BEM≌△HEM,
∴BM=HM,∠EBM=∠EHM=45°,
∴∠NHM=90°
∴线段BM、MN、DN为三边构成的是一个直角三角形
【解析】(1)由条件直接证明三角形全等就可以得出CE=CF.(2)由条件和(1)的结论可以证明三角形ECG全等三角形FCG,可以得出EG=FG,可以得出GE=BE+GD.(3)先判断出△DGN≌△HGN得到结论,再判断出△BEM≌△HEM,最后简单计算即可.
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案