题目内容
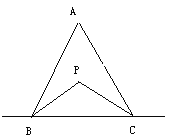
【题目】如图,已知点A在直线l外,点B、C在直线l上.
(1)点P是△ABC内一点,求证:∠P>∠A;
(2)试判断:在△ABC外又和点A在直线l同侧,是否存在一点Q,使∠BQC>∠A?试证明你的结论.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)延长BP交AC于D,运用三角形的外角大于与它不相邻的内角即可证明;
(2)在直线l同侧,且在△ABC外,存在点Q,使得∠BQC>∠A成立.
试题解析:(1)延长BP交AC于D,则∠BPC>∠BDC,∠BDC>∠A故∠BPC>∠A;
(2)在直线l同侧,且在△ABC外,存在点Q,使得∠BQC>∠A成立.此时,只需在AB外,靠近AB中点处取点Q,则∠BQC>∠A.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是。
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
频数 | 9 | 15 | ? | 16 | 12 |
【题目】如表是小明同学参加“一分钟汉字听写”训练近6次的成绩:
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
听写字数 | 245 | 248 | 240 | 243 | 246 | 242 |
则这组数据的平均数和中位数分别是( )
A. 245个、244个B. 244个、244个
C. 244个、241.5个D. 243个、244个