题目内容
如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若S四边形AEOH＝3，S四边形BFOE＝4，S四边形CGOF＝5，则S四边形DHOG＝________．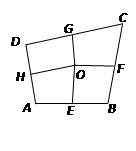
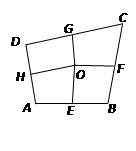
4
连接OC，OB，OA，OD，∵E、F、G、H依次是各边中点，
∴△AOE和△BOE等底等高，所以S△OAE=S△OBE，
同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，
∵S四边形AEOH=3，S四边形BFOE=4，S四边形CGOF=5，∴3+5=4+S四边形DHOG，解得，S四边形DHOG=4．
∴△AOE和△BOE等底等高，所以S△OAE=S△OBE，
同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，
∵S四边形AEOH=3，S四边形BFOE=4，S四边形CGOF=5，∴3+5=4+S四边形DHOG，解得，S四边形DHOG=4．
练习册系列答案
相关题目
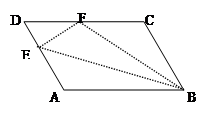
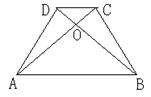
中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，当E、F满足下列哪个条件时，四边形DEBF不一定是平行四边形……（ ▲ ）
。
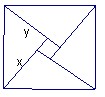
；②x-y=2；③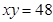
；④x+y="14." 其中说法正确的是 （只填序号）
