题目内容
【题目】如图,四边形ABCD是正方形,△PAD是等边三角形,则∠BPC等于( )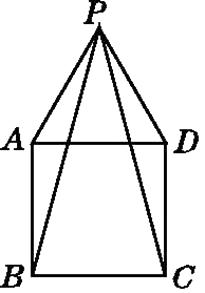
A.20°
B.30°
C.35°
D.40°
【答案】B
【解析】∵四边形ABCD是正方形,△PAD是等边三角形,∴∠BAP=∠BAD+∠PAB=90°+60°=150°, PA=AD,AB=AD,
∴PA=AB,
∴∠ABP= ![]() =15°,
=15°,
∴∠PBC=∠ABC-∠ABP=90°-15°=75°,
同理:∠PCB=75°,
∴∠BPC=180°-75°-75°=30°.
故应选 :B 。
根据正方形及等边三角形的性质得出∠BAP=∠BAD+∠PAB=90°+60°=150°, PA=AD,AB=AD,利用等量代换得出PA=AB ,根据等腰三角形底角的计算方法得出∠ABP的度数,根据角的和差得出∠PBC=∠ABC-∠ABP=90°-15°=75°,同理:∠PCB=75° ,从而利用三角形的内角和得出∠BPC=180°-75°-75°=30°.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目