题目内容
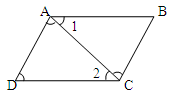
如图，AB=AC， AD∥BC，∠BAC=100°，则∠CAD的度数是（ ）
| A．30° | B．35° | C．40° | D．50° |
C．
解析试题分析：根据等腰三角形性质，三角形内角和定理求出∠C，根据平行线的性质得出∠CAD=∠C，即可求出答案:
∵AB=AC，∠BAC=100°，∴∠B=∠C=40°.
∵AD∥BC，∴∠CAD=∠C=40°.
故选C．
考点：1.平行线的性质；2.等腰三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
下列四个图中，∠1和∠2是对顶角的图的个数是( )
| A．0个 | B．1个 | C．2个 | D．3个 |
如图，已知AB∥CD，∠1=62°，则∠2的度数是（ ）
| A．28° | B．62° | C．108° | D．118° |
下列说法正确的是( )
| A．内错角相等 |
| B．任何数的0次方都等于1 |
| C．一个角的补角一定大于它本身 |
| D．平行于同一直线的两条直线互相平行 |
如图，直线l1∥l2，∠1=∠2=35°，∠P=90°，则∠3等于（ ）
| A．50° | B．55° | C．60° | D．65° |
