题目内容
如图，直线l1∥l2，∠1=∠2=35°，∠P=90°，则∠3等于（ ）
| A．50° | B．55° | C．60° | D．65° |
B．
解析试题分析：先根据两直线平行，同旁内角互补，求出∠3与∠4的和，再根据直角三角形两锐角互余求出∠4，∠3即可求得：
如图，∵l1∥l2，∴∠1+∠2+∠3+∠4=180°.
∵∠1=∠2=35°，∴∠3+∠4=110°.
∵∠P=90°，∠2=35°，∴∠4=90°-35°=55°.
∴∠3=110°-55°=55°．
故选B．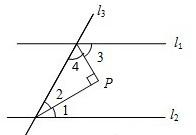
考点：1.平行线的性质；2.直角三角形的性质．
练习册系列答案
名校课堂系列答案
相关题目
如图，AB=AC， AD∥BC，∠BAC=100°，则∠CAD的度数是（ ）
| A．30° | B．35° | C．40° | D．50° |
如图，点
在
的延长线上，下列条件中能判断AB//CD的是（ ）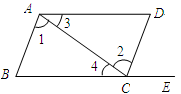
| A．∠3=∠4 | B．∠D=∠DCE |
| C．∠B=∠D | D．∠1=∠2 |
下例命题不是真命题的是（ ）
| A．垂直于同一条直线的两直线平行 |
| B．同旁内角互补 |
| C．两点之间，线段最短 |
| D．同角的余角相等 |
下列说法正确的是（ ）
| A．相等的角是对顶角 | B．同位角相等 |
| C．两直线平行，同旁内角相等 | D．同角的补角相等 |
如图，∠1=∠2，∠3=40°，则∠4等于（ ）
| A．120° | B．130° | C．140° | D．40° |
如图两平行线a、b被直线l所截，且∠1=60°，则∠2的度数为( )
| A．30 | B．45° | C．60° | D．120° |
