题目内容
【题目】如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y=![]() 的图象在第一象限内的交点为M,若△OBM的面积为1.
的图象在第一象限内的交点为M,若△OBM的面积为1.

(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】(1)反比例函数解析式为:y=![]() ;(2)P(5,0);(3)Q点坐标为:(
;(2)P(5,0);(3)Q点坐标为:(![]() ,0).
,0).
【解析】
试题(1)利用已知点B坐标代入一次函数解析式得出答案,再利用△OBM的面积得出M点纵坐标,再利用相似三角形的判定与性质得出M点坐标即可得出反比例函数解析式;
(2)过点M作PM⊥AM,垂足为M,得出△AOB∽△PMB,进而得出BP的长即可得出答案;
(3)利用△QBM∽△OAM,得出![]() =
=![]() ,进而得出OQ的长,即可得出答案.
,进而得出OQ的长,即可得出答案.
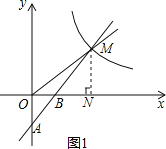
解:(1)如图1,过点M作MN⊥x轴于点N,
∵一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,
∴0=k1﹣1,AO=BO=1,
解得:k1=1,
故一次函数解析式为:y=x﹣1,
∵△OBM的面积为1,BO=1,
∴M点纵坐标为:2,
∵∠OAB=∠MNB,∠OBA=∠NBM,
∴△AOB∽△MNB,
∴![]() =
=![]() =
=![]() ,
,
则BN=2,
故M(3,2),
则xy=k2=6,
故反比例函数解析式为:y=![]() ;
;
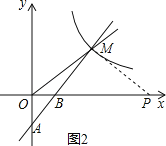
(2)如图2,过点M作PM⊥AM,垂足为M,
∵∠AOB=∠PMB,∠OBA=∠MBP,
∴△AOB∽△PMB,
∴![]() =
=![]() ,
,
由(1)得:AB=![]() =
=![]() ,BM=
,BM=![]() =2
=2![]() ,
,
故![]() =
=![]() ,
,
解得:BP=4,
故P(5,0);
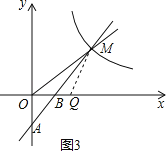
(3)如图3,∵△QBM∽△OAM,
∴![]() =
=![]() ,
,
由(2)可得AM=3![]() ,
,
故![]() =
=![]() ,
,
解得:QB=![]() ,
,
则OQ=![]() ,
,
故Q点坐标为:(![]() ,0).
,0).

【题目】某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 | 乙 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过500棵时 | 800元/棵 | 不超过1000棵时 | 800元/棵 |
超过500棵的部分 | 700元/棵 | 超过1000棵的部分 | 600元/棵 |
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?