题目内容
(2011•攀枝花)如图,已知直线l1: 与直线 l2:y=﹣2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=﹣2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .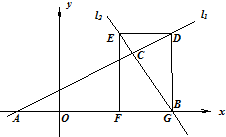
 与直线 l2:y=﹣2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=﹣2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
8:9
由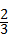 x+
x+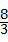 =0,得x=﹣4.
=0,得x=﹣4.
∴A点坐标为(﹣4,0),
由﹣2x+16=0,得x=8.
∴B点坐标为(8,0),
∴AB=8﹣(﹣4)=12.
由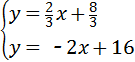 ,解得
,解得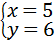 ,
,
∴C点的坐标为(5,6),
∴S△ABC=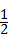 AB•C=
AB•C=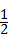 ×12×6=36.
×12×6=36.
∵点D在l1上且xD=xB=8,
∴yD=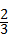 ×8+
×8+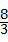 =8,
=8,
∴D点坐标为(8,8),
又∵点E在l2上且yE=yD=8,
∴﹣2xE+16=8,
∴xE=4,
∴E点坐标为(4,8),
∴DE=8﹣4=4,EF=8.
∴矩形面积为:4×8=32,
∴S矩形DEFG:S△ABC=32:36=8:9.
故答案为:8:9.
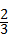 x+
x+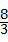 =0,得x=﹣4.
=0,得x=﹣4.∴A点坐标为(﹣4,0),
由﹣2x+16=0,得x=8.
∴B点坐标为(8,0),
∴AB=8﹣(﹣4)=12.
由
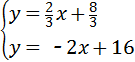 ,解得
,解得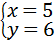 ,
,∴C点的坐标为(5,6),
∴S△ABC=
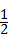 AB•C=
AB•C=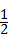 ×12×6=36.
×12×6=36.∵点D在l1上且xD=xB=8,
∴yD=
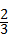 ×8+
×8+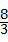 =8,
=8,∴D点坐标为(8,8),
又∵点E在l2上且yE=yD=8,
∴﹣2xE+16=8,
∴xE=4,
∴E点坐标为(4,8),
∴DE=8﹣4=4,EF=8.
∴矩形面积为:4×8=32,
∴S矩形DEFG:S△ABC=32:36=8:9.
故答案为:8:9.

练习册系列答案
相关题目
 千米/分钟,甲到达B地立即返回.乙所乘冲锋舟在在静水中的速度
千米/分钟,甲到达B地立即返回.乙所乘冲锋舟在在静水中的速度 为
为 千米/分钟.已知A、B两地的距离为20千米,水流速度为
千米/分钟.已知A、B两地的距离为20千米,水流速度为 千米/分钟,甲、乙乘冲锋舟行驶的距离y(千米)与所用时间x(分钟)之间的函数图象如图所示.
千米/分钟,甲、乙乘冲锋舟行驶的距离y(千米)与所用时间x(分钟)之间的函数图象如图所示.
 程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
程s与时间t之间的图象,并结合图象直接写出三轮车追上师生时,离学校的路程;
 x+3的坐标三角形的三条边长; (2)若
x+3的坐标三角形的三条边长; (2)若
 中,AB=AC=2,
中,AB=AC=2, ,
, 是
是 边上一个动点,过点
边上一个动点,过点
 ,交
,交 .若设
.若设 ,
, 的面积为
的面积为 ,则
,则

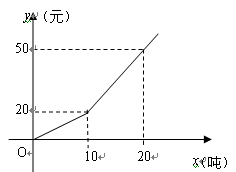
 (元)出租车行驶路线
(元)出租车行驶路线 (km)之间的关系式(其中
(km)之间的关系式(其中 )
)