题目内容
【题目】如图,直线l1:y=mx+4m与x轴负半轴、y轴正半轴分别交于A、B两点.
(1)如图(1),当OA=OB时,求直线l1的解析式;
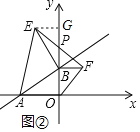
(2)如图(2),当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为腰,点B为直角顶点在第一、二象限作等腰直角△OBF和等腰直角△ABE,连接EF交y轴于点P,试猜想PB的长是否为定值?若是,求出其值;若不是,说明理由.
(3)m取不同的值时,点B在y轴正半轴上运动,以AB为腰,点B为直角顶点在第二象限作等腰直角△ABD,满足条件的动点D在直线l2上运动,直线l2与x轴和y轴分别交于F、H两点,若直线l1将△OHF分成面积比为m:1的两部分,求此时直线l1和直线l2的解析式.

【答案】(1)y=x+4;(2)PB的长为定值,理由见解析;(3)直线l1的解析式为:y=![]() x+6-2
x+6-2![]() ,直线l2的解析式为:y=-x+4
,直线l2的解析式为:y=-x+4
【解析】
(1)由直线![]() 解析式,求出A与B坐标,根据OA=OB,求出m的值,即可确定出直线L解析式;
解析式,求出A与B坐标,根据OA=OB,求出m的值,即可确定出直线L解析式;
(2)过点E作EG⊥y轴于G点,先证明△ABO≌△EGB,从而得到BG=4,然后证明△BFP≌△GEP,从而得到BP=GP=![]() BG;
BG;
(3)如图③,由A(-4,0),B(0,4m),得到OA=BG=4,DG=OB=4m,得到点D(-4m,4m+4),于是求得直线![]() 的解析式为:
的解析式为:![]() 根据三角形的面积公式列方程即可得到结论.
根据三角形的面积公式列方程即可得到结论.
解:(1)∵直线l1:y=mx+4m与x轴负半轴、y轴正半轴分别交于A、B两点,
∴A(-4,0),B(0,4m),
由OA=OB,得4m=4,m=1,
∴直线解析式为:y=x+4;
(2)PB的长为定值.
理由:如图②所示:过点E作EG⊥y轴于G点.
∵△AEB为等腰直角三角形,
∴AB=EB,∠ABO+∠EBG=90°.
∵EG⊥BG,
∴∠GEB+∠EBG=90°.
∴∠ABO=∠GEB.
在△ABO和△EGB中,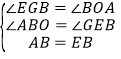 ,
,
∴△ABO≌△EGB.(AAS)
∴BG=AO=4,OB=EG
∵△OBF为等腰直角三角形,
∴OB=BF
∴BF=EG.
在△BFP和△GEP中,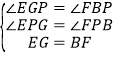 ,
,
∴△BFP≌△GEP.(AAS)
∴BP=GP=![]() BG=2是定值;
BG=2是定值;
(3)如图③,
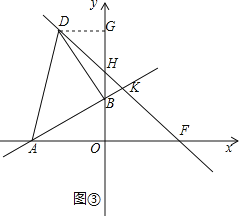
∵A(-4,0),B(0,4m),
由(2)证得OA=BG=4,DG=OB=4m,
∴OG=OB+BG=4m+4,
∴点D(-4m,4m+4),
∵动点D在直线y=-x+4上运动,
∴直线l2的解析式为:y=-x+4,
∴F(4.0),H(0,4),
∴S△OHF=![]() ×4×4=8,
×4×4=8,
设直线l1和直线l2的交点为K,
解![]() 得,
得,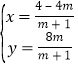 ,
,
∴K(![]() ,
,![]() ),
),
∵直线l1将△OHF分成面积比为m:1的两部分,
∴当S△HBK:S四边形OFKB=m:1时,
S△HBK=![]() (4-4m)
(4-4m)![]() =8×
=8×![]() ,
,
解得:m=![]() ,m=
,m=![]() ,
,
当S△HBK:S四边形OFKB=1:m时,
S△HBK=![]() (4-4m)
(4-4m)![]() =8×
=8×![]() ,
,
解得:m=2,m=0,
∵4m<4,且m≠0,
∴m=![]() ,
,
∴直线l1的解析式为:y=![]() x+6-2
x+6-2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 |
|
|
|
|
|
小夏 |
|
|
|
|
|
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 |
|
|
| |
小夏 |
|
|
|
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是![]() 分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(
分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)(![]() )
)
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
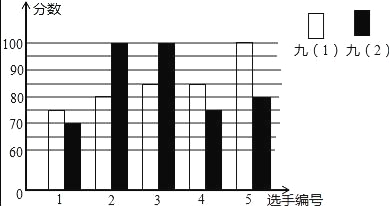
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
九(1) | 85 | |
九(2) | 100 |
(2)通过计算得知九(2)班的平均成绩为85分,请计算九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?