题目内容
【题目】如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.
【答案】解:作CD⊥AB于D,如图, 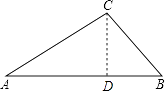
在Rt△ACD中,∵∠A=30°,
∴CD= ![]() AC=1,AD=
AC=1,AD= ![]() CD=
CD= ![]() ,
,
在Rt△CBD中,∵∠B=45°,
∴BD=CD=1,CB= ![]() AD=
AD= ![]() ,
,
∴BA=BD+AD=1+ ![]() ,
,
∴△ABC的周长=AB+AC+BC= ![]() +2+1+
+2+1+ ![]() =3+
=3+ ![]() .
.
△ABC的面积= ![]() ADBC=
ADBC= ![]() 1(
1( ![]() +1)=
+1)= ![]() .
.
答:△ABC的周长为3+ ![]() ,△ABC的面积为
,△ABC的面积为 ![]() .
.
【解析】通过做辅助线,得到直角三角形,根据直角三角形的性质∠A=30°,得到CD=![]() ,AD=
,AD= ![]() CD=
CD= ![]() ,由∠B=45°,得到BD=CD=1,CB=
,由∠B=45°,得到BD=CD=1,CB=![]() AD=
AD=![]() ,求出BA=1+
,求出BA=1+![]() ,得到 ABC的周长=3+
,得到 ABC的周长=3+![]() +
+![]() , △ABC的面积=
, △ABC的面积=![]() ADBC.
ADBC.
【考点精析】关于本题考查的三角形的面积和勾股定理的概念,需要了解三角形的面积=1/2×底×高;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

练习册系列答案
相关题目