题目内容
如图,针孔成像问题,AB∥A’B’,根据图中尺寸,物像长y与物长x之间函数关系的图象大致是
( )
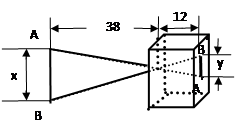

( )
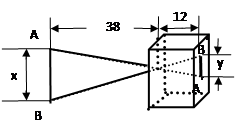

D
考点:
专题:几何图形问题.
分析:可利用相似三角形的性质,即对应边上高的比等于相似比,得出函数关系式,结合自变量的取值范围判断函数图象.
解答:解:∵AB∥A′B′,
∴△OAB∽△OA′B′,
∴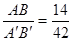 ,即
,即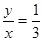
∴y=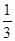 x (x>0),是正比例函数,
x (x>0),是正比例函数,
图象为不包括原点的射线.
故选D.
点评:主要是读懂题意图意,找到相应的等量关系是解决本题的关键.
专题:几何图形问题.
分析:可利用相似三角形的性质,即对应边上高的比等于相似比,得出函数关系式,结合自变量的取值范围判断函数图象.
解答:解:∵AB∥A′B′,
∴△OAB∽△OA′B′,
∴
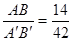 ,即
,即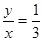
∴y=
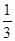 x (x>0),是正比例函数,
x (x>0),是正比例函数,图象为不包括原点的射线.
故选D.
点评:主要是读懂题意图意,找到相应的等量关系是解决本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 在函数
在函数 的图象上,那么点P应在平面直角坐标系中的【 】
的图象上,那么点P应在平面直角坐标系中的【 】

 ,则下列函数:①
,则下列函数:① ,②
,②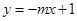 ,③
,③ ,
, 中,
中, 随
随 的增大而增大的函数有( ▲ )
的增大而增大的函数有( ▲ )

 中,自变量
中,自变量 的取值范围是______________.
的取值范围是______________.