Question

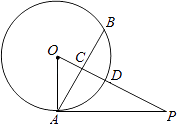
【题目】如图1，在△ABC中，AB=AC=8cm，BC=6cm，D为AB中点，点P在AC上从C向A运动，运动速度为2（cm/s）；同时，点Q在BC上从B向C运动，设点Q的运动速度为x（cm/s）．且设P，Q的运动时间均为t秒，若其中一点先到达终点，则另一个点也将停止运动．

（1）如图2，当PD∥BC时，请解决下列问题：

①t=　 　；

②△ADP的形状为　 　（按“边”分类）；

③若此时恰好有△BDQ≌△CPQ，请求出点Q运动速度x的值；

（2）当PD与BC不平行时，也有△BDQ与△CPQ全等：

①请求出相应的t与x的值；

②若设∠A=α°，请直接写出相应的∠DQP的度数（用含α的式子表示）．

Answer 1

【答案】（1）①2；②等腰三角形；③1.5cm/s；（2）①当t=1时，x=2；当t=2时，x=3；②.

【解析】

（1）①根据三角形中位线的性质得到当P为AC的中点时，PD∥BC，求出AP，即可解答；②△ADP的形状为等腰三角形，证明AD＝AP，即可解答；③根据全等三角形的对应边相等，得到BQ＝CQ，即可解答；（2）①求出BD，根据全等得出要使△BPD与△CQP全等，必须BD＝CP或BP＝CP，得出方程12＝16－4x或4x＝16－4x，求出方程的解即可；②先利用定义三角形的性质求出∠B的性质，再由△BDQ与△CPQ全等，∠BDQ＝∠PQC，由∠B＋∠BDQ＋∠BQD＝180°，∠DQP＋∠PQC＋∠BQD＝180°，得到∠DQB＋∠B，即可解答.

（1）①∵PD∥BC，D为AB中点，

∴点P为AC的中点，

∴AP=CP= AC==4cm，

∴t=4÷2=2．

故答案为：2；

②∵D为AB中点，点P为AC的中点，AB=AC，

∴AD=AP，

∴△ADP为等腰三角形，

故答案为：等腰三角形；

③如图2，

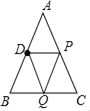
∵△BDQ≌△CPQ，

∴BQ=CQ，

∴BQ=BC= =3cm，

∴点Q运动速度x的值为：3÷2=1.5（cm/s）；

（2）如图3，

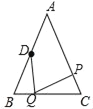
设经过t秒后，使△BPD与△CQP全等，

∵AB=AC=12，点D为AB的中点，

∴BD=6，

∵∠ABC=∠ACB，

∴要使△BPD与△CQP全等，必须BD=CP或BP=CP，

即6=8﹣2t或2t=8﹣2t，

t1=1，t2=2，

t=1时，BP=CQ=2，2÷1=2；

t=2时，BD=CQ=6，6÷2=3；

∴当t=1时，x=2；当t=2时，x=3．

②∵AB=AC，∠A=α°，

∴∠B=∠C=，

∵△BDQ与△CPQ全等，

∴∠BDQ=∠PQC，

∵∠B+∠BDQ+∠BQD=180°，

∠DQP+∠PQC+∠BQD=180°，

∴∠DQB=∠B=．