Question

【题目】在平面直角坐标系xOy中，抛物线y=ax2+bx+c经过点（1，2），（5，3），则下列说法正确的是（　　）

①抛物线与y轴有交点

②若抛物线经过点（2，2），则抛物线的开口向上

③抛物线的对称轴不可能是x=3

④若抛物线的对称轴是x=4，则抛物线与x轴有交点

A.①②③④B.①②③C.①③④D.②④

Answer 1

【答案】A

【解析】

①当x=0时，y=c，与y轴有交点②将点（1，2），（2，2），（5，3）代入解析式，得到a=，③如果抛物线的对称轴x=3，（1，2）关于对称轴对称的点为（5，2），与经过点（5，3）矛盾，④对称轴是x=4，a=-，b=1，c=，△=b2-4ac=64a2-4ac＞0.

①当x=0时，y=c，∴与y轴有交点；①正确；

②抛物线经过（1，2），（2，2），（5，3），

∴，

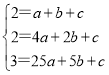∴a=，

∴抛物线开口向上；

∴②正确；

③如果抛物线的对称轴x=3，

（1，2）关于对称轴对称的点为（5，2），

与经过点（5，3）矛盾，

∴对称轴不能是x=3，

∴③正确；

④对称轴是x=4，

∴-=4，

∴b=-8a，

将点（1，2），（5，3）代入得，

，

∴24a+4b=1，

∴-8a=1，

∴a=-，

∴b=1，c=

△=b2-4ac=64a2-4ac＞0，

∴抛物线与x轴有交点，

∴④正确；

故选：A．