Question

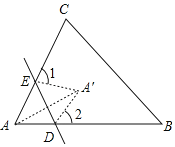
【题目】如图，△ABC中，点D，E分别在边AB，AC上，将∠A沿着DE所在直线折叠，A与A′重合，若∠1+∠2＝140°，则∠A的度数是（　　）

A.70°B.75°C.80°D.85°

Answer 1

【答案】A

【解析】

连接AA'，依据∠1是△AA'E的外角，可得∠1＝∠EAA'+∠EA'A，同理可得∠2＝∠DAA'+∠DA'A，由折叠的性质得出∠EAD＝∠EA'D，再依据角的和差关系进行计算即可．

解：连接AA'，如图所示：

∵∠1是△AA'E的外角，∴∠1＝∠EAA'+∠EA'A，

同理可得，∠2＝∠DAA'+∠DA'A，

由折叠可得，∠EAD＝∠EA'D，

∴∠1+∠2＝∠EAA'+∠EA'A+∠DAA'+∠DA'A＝2∠EAD＝140°，

∴∠EAD＝70°.

故选：A．