Question

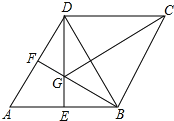
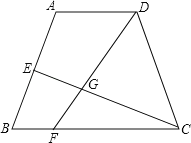
【题目】如图，已知等腰梯形ABCD中，AD∥BC，AD：BC＝1：2，点E为边AB中点，点F是边BC上一动点，线段CE与线段DF交于点G．

（1）若，求的值；

（2）连接AG，在（1）的条件下，写出线段AG和线段DC的位置关系和数量关系，并说明理由；

（3）连接AG，若AD＝2，AB＝3，且△ADG与△CDF相似，求BF的长．

Answer 1

【答案】（1）；（2）AG∥DC，且；理由见解析；（3）BF＝1．

【解析】

（1）延长CE和DA，相交于M，根据平行线分线段成比例进行计算可以求出的值；

（2）在（1）的条件下，求出，根据对应线段的比相等可以得到AG与DC的位置和数量关系；

（3）根据∠ADG＝∠DFC分两种情况讨论：①当∠AGD＝∠FDC，即△ADG∽△CFD时，②当∠DAG＝∠FDC时，分别求解即可．

解：（1）∵BF：FC＝1：3，

∴设BF＝k，则FC＝3k，BC＝4k，

∵AD：BC＝1：2，

∴AD＝2k，

如图：延长CE交DA的延长线于点M，

∵AD∥BC，

∴，且，

∵点E为边AB中点，

∴AM＝BC＝4k，

∴DM＝DA+AM＝2k+4k＝6k，

∴；

（2）AG∥DC，且．

证明：∵AD∥BC，

∴，

∵，

∴，

∴AG∥DC，

∴；

（3）∵ABCD是等腰梯形，AD＝2，AD：BC＝1：2，

∴BC＝4，

∵AD∥BC，

∴∠ADG＝∠DFC，

∵△ADG和△CDF相似，

∴∠AGD＝∠FDC或∠DAG＝∠FDC，

①当∠AGD＝∠FDC，即△ADG∽△CFD时，有AG∥DC，延长CE交DA的延长线于点M，可得AM＝4，

由得，

∴AG＝2，

∵△ADG∽△CFD，

∴，即，

∴CF＝3，

∴BF＝1；

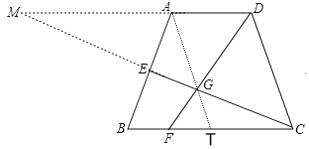
②当∠DAG＝∠FDC时，延长AG交BC于点T，

∵∠ATB＝∠DAG＝∠FDC，∠B＝∠C，

∴△ABT∽△FCD，

∴，

由AD∥BC得，

设BF＝x，

则，

∴FT＝，

∴，

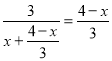整理得：2x2﹣4x+11＝0，

∵△＝16﹣88＜0，

∴无实数根，即此情况不存在；

综上所述，BF＝1．