题目内容
【题目】在△ABC中,AD平分∠BAC交BC于点D.
(1)在图1中,将△ABD沿BC的方向平移,使点D移至点C的位置,得到△A′B′D′,且A′B′交AC于点E,猜想∠B′EC与∠A′之间的关系,并说明理由; 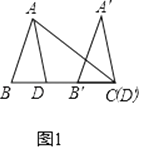
(2)在图2中,将△ABD沿AC的方向平移,使A′B′经过点D,得到△A′B′D′,求证:A′D′平分∠B′A′C. 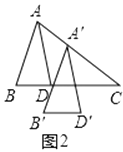
【答案】
(1)证:∠B′EC=2∠A′,其理由是:
∵△A′B′D′是由△ABD平移而来,
∴A′B′∥AB,∠A′=∠BAD.
∴∠B′EC=∠BAC.
∵AD平分∠BAC,
∴∠BAC=2∠BAD.
∴∠B′EC=2∠A′.
(2)证:∵△A′B′D′是由△ABD平移而来,
∴A′B′∥AB,∠B′A′D′=∠BAD.
∴∠B′A′C=∠BAC.
∵AD平分∠BAC,∴∠BAC=2∠BAD.
∴∠B′A′C═2∠B′A′D′.
∴A′D′平分∠B′A′C.
【解析】(1)根据平移的性质得到A′B′∥AB,∠A′=∠BAD,从而得到∠B′EC=∠BAC,然后根据AD平分∠BAC得到∠BAC=2∠BAD,从而得到∠B′EC=2∠A′;(2)根据平移的性质得到A′B′∥AB,∠B′A′D′=∠BAD,进一步得到∠B′A′C=∠BAC,然后根据AD平分∠BAC得到∠BAC=2∠BAD,从而得到∠B′A′C═2∠B′A′D′.
【考点精析】本题主要考查了平移的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.

练习册系列答案
相关题目