题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 于
于![]() .
.
(1)求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)60°;(2)6
【解析】
(1)根据![]() ,
,![]() 求出∠C,然后根据直角三角形的两锐角互余求出
求出∠C,然后根据直角三角形的两锐角互余求出![]() 的度数;
的度数;
(2)连接AD,根据三线合一得到AD垂直于BC,AD为角平分线,在直角三角形ADE中,利用30角所对的直角边等于斜边的一半得到AD的长,在直角三角形ADC中,再利用30角所对的直角边等于斜边的一半求出AC的长,由AC-AE即可求出CE的长.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)连接AD,
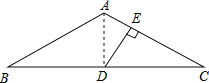
∵AB=AC,∠BAC=120°,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,
∴∠DAC=![]() ∠BAC=60°,
∠BAC=60°,
∵DE⊥AC于E,
∴∠AED=90°,
∴∠ADE=30°,
在Rt△ADE中,AE=2,∠ADE=30°,
∴AD=2AE=4,
在Rt△ADC中,AD=4,∠C=30°,
∴AC=2AD=8,则CE=ACAE=82=6.

练习册系列答案
相关题目