题目内容
【题目】某巡警骑摩托车在一条南北大道上巡逻．某天他从岗亭出发，晚上停留在A处．规定向北方向为正．当天行驶记录如下（单位：千米）．
+10，﹣8，+6，﹣13，+7，﹣12，+3，﹣2
（1）以岗亭为原点，用1个单位长度表示1KM,，在数轴上表示，A在岗亭何方，有多远？
（2）为该巡警巡逻时离岗亭最远是多少千米？
（3）在岗亭北面6千米处有个加油站，该巡警巡逻时经过加油站几次？
（4）若摩托车每行1千米耗油0.05升，那么该摩托车这天巡逻共耗油多少升？
【答案】（1）数轴见解析，A在岗亭南方9km处；（2）该巡警巡逻时离岗亭最远是10千米；（3）该巡警巡逻时经过加油站4次；（4）该摩托车这天巡逻共耗油3.05升.
【解析】
（1）求出行驶记录的和，在数轴上表示出A处的位置，然后进行判断；
（2）求出每次行驶后所在位置，然后判断即可；
（3）根据行驶记录，依次计算是否经过加油站即可；
（4）求出各数据绝对值之和，乘以0.05即可得到结果．
解：（1）∵10+（-8）+6+（-13）+7+（-12）+3+（-2）=－9，
在数轴表示如图：
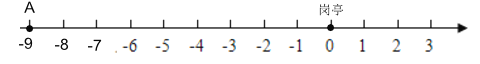
∴A在岗亭南方9km处；
（2）∵10，108＝2，2＋6＝8，813＝5，5＋7＝2，212＝10，10＋3＝7，72＝9，
∴该巡警巡逻时离岗亭最远是10千米；
（3）第一次向北行驶10km，此时第一次经过加油站，
第二次往回走8km，第二次经过加油站，
第三次向北行驶6km，10-8+6=8＞6，第三次经过加油站，
第四次往回走13km，8-13=-5，第四次经过加油站，
第五次向北行驶7km,-5+7=2＜6，所以不经过加油站，
第五次以后向南行驶距离较长，向北行驶距离较短，不会再经过加油站，
故该巡警巡逻时经过加油站4次；
（4）10+|﹣8|+6+|﹣13|+7+|﹣12|+3+|﹣2|=61km，
61×0.05=3.05（升），
答：该摩托车这天巡逻共耗油3.05升.
永乾教育寒假作业快乐假期延边人民出版社系列答案
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润=收入﹣成本），并指出售价为多少元时获得最大利润，最大利润是多少？
【题目】李先生在2019年10月第2周星期五股市收盘时，以每股9元的价格买进某公司的股票1000股，在11月第2周的星期一至星期五，该股票每天收盘时每股的涨跌（单位：元）情况如下表：
时 间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
每股涨跌/元 | 0 | -0.32 | +0.47 | -0.21 | +0.56 |
注：表中记录的数据为每天收盘价格与前一天收盘价格的变化量，星期一的数据是与上星期五收盘价格的变化量．
（1）请你判断在11月的第2周内，该股票价格收盘时，价格最高的是哪一天？
（2）在11月第2周内，求李先生购买的股票每股每天平均的收盘价格．（结果精确到百分位）
