题目内容
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)
的左边)![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() 为抛物线的顶点.
为抛物线的顶点.
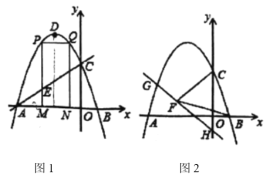
(1)求抛物线的解析式;
(2)点![]() 为线段
为线段![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,可得矩形
,可得矩形![]() ,如图1,点
,如图1,点![]() 在点
在点![]() 左边,当矩形
左边,当矩形![]() 的周长最大时,求
的周长最大时,求![]() 的值,并求出此时的
的值,并求出此时的![]() 的面积;
的面积;
(3)已知![]() ,点
,点![]() 在抛物线上,连
在抛物线上,连![]() ,直线
,直线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)y=x22x+3(2)m=2,S△AEM=![]() (3)(
(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x1,再根据OC=OA,AB=4,可得A(3,0),最后代入抛物线y=ax2+2ax+3,得抛物线的解析式为y=x22x+3;
(2)根据点M(m,0),可得矩形PQNM中,P(m,m22m+3),Q(2m,m22m+3),再根据矩形PQNM的周长=2(PM+PQ)=2(m+2)2+10,可得当m=2时,矩形PQNM的周长有最大值10,M的坐标为(2,0),最后由直线AC为y=x+3,AM=1,求得E(2,1),ME=1,据此求得△AEM的面积;
(3)连接CB并延长,交直线HG与Q,根据已知条件证明BC=BF=BQ,再根据C(0,3),B(1,0),得出Q(2,3),根据H(0,1),求得QH的解析式为y=x1,联立得到方程组,可解得点G的坐标.
(1)由抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x=![]() =1,
=1,
∵OC=OA,
∴A(c,0),B(2+c,0),
∵AB=4,
∴2+c(c)=4,
∴c=3,
∴A(3,0),
代入抛物线y=ax2+2ax+3,得
0=9a6a+3,
解得a=1,
∴抛物线的解析式为y=x22x+3;
(2)如图1,∵M(m,0),PM⊥x轴,
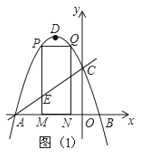
∴P(m,m22m+3),
又∵对称轴为x=1,PQ∥AB,
∴Q(2m,m22m+3),
又∵QN⊥x轴,
∴矩形PQNM的周长
=2(PM+PQ)
=2[(m22m+3)+(2mm)]
=2(m24m+1)
=2(m+2)2+10,
∴当m=2时,矩形PQNM的周长有最大值10,
此时,M(2,0),
设直线AC的解析式为y=kx+b
把A(3,0),C(0,3)代入得![]()
解得![]()
∴直线AC为y=x+3,又AM=1,
∴当x=2时,y=1,即E(2,1),ME=1,
∴△AEM的面积=![]() ×AM×ME=
×AM×ME=![]() ×1×1=
×1×1=![]() ;
;
(3)如图2,连接CB并延长,交直线HG与Q,

∵HG⊥CF,BC=BF,
∴∠BFC+∠BFQ=∠BCF+∠Q=90![]() ,∠BFC=∠BCF,
,∠BFC=∠BCF,
∴∠BFQ=∠Q,
∴BC=BF=BQ,
∴C,Q关于B点对称
又∵C(0,3),B(1,0),
∴Q(2,3),
又∵H(0,1)
设QH的解析式为y=px+q,
把Q(2,3),H(0,1)代入得![]()
解得![]()
∴QH的解析式为y=x1,
解方程组![]() ,可得
,可得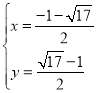 或
或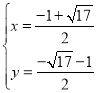 ,
,
∴点G的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 名校课堂系列答案
名校课堂系列答案【题目】嘉善县将开展以“珍爱生命,铁拳护航”为主题的交通知识竞赛,某校对参加选拔赛的若干名同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
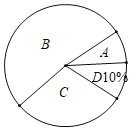
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应圆心角的度数;
(3)“A等级”的4名同学中有3名男生和1名女生,现从中随机挑选2名同学代表学校参加全县比赛,请用树状图法或列表法求出恰好选中“一男一女”的概率.
【题目】如图,有长为![]() 的篱笆,现一面利用墙(墙的最大可用长度
的篱笆,现一面利用墙(墙的最大可用长度![]() 为
为![]() )围成中间隔有一道篱笆的长方形花圃,设花圃的宽
)围成中间隔有一道篱笆的长方形花圃,设花圃的宽![]() 为
为![]() ,面积为
,面积为![]() .
.

(1)求![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)要围成面积为![]() 的花圃,
的花圃,![]() 的长是多少米?
的长是多少米?
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表:
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |
请根据图表中提供的信息回答下列问题:
(1)统计表中的a=______,b=______;
(2)“陶艺制作”对应扇形的圆心角为______;
(3)根据调查结果,请你估计该校300名学生中最喜欢“智能机器人”创客课程的人数;
(4)学校为开设这四门课程,预计每生A、B、C、D四科投资比为4:3:6:7,若“3D打印课程每人投资200元,求学校为开设创客课程,需为学生人均投入多少钱?