Question

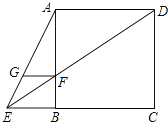
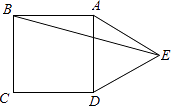
【题目】如图，四边形ABCD是矩形，点E在BC边上，点F在BC延长线上，且∠CDF=∠BAE．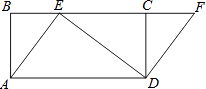
（1）求证：四边形AEFD是平行四边形；
（2）若DF=3，DE=4，AD=5，求CD的长度．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AB=DC，∠B=∠DCF=90°，

∵∠BAE=∠CDF，

在△ABE和△DCF中，

，

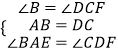∴△ABE≌△DCF（ASA），

∴BE=CF，

∴BC=EF，

∵BC=AD，

∴EF=AD，

又∵EF∥AD，

∴四边形AEFD是平行四边形

（2）解：由（1）知：EF=AD=5，

在△EFD中，∵DF=3，DE=4，EF=5，

∴DE2+DF2=EF2，

∴∠EDF=90°，

∴ EDDF= EFCD，

∴CD= ．

【解析】（1）直接利用矩形的性质结合全等三角形的判定与性质得出BE=CF，进而得出答案；（2）利用勾股定理的逆定理得出∠EDF=90°，进而得出 EDDF= EFCD，求出答案即可．