题目内容
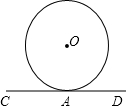 如图,石景山游乐园的观览车半径为25m,已知观览车绕圆心O顺时针做匀速运动,旋转一周用12分钟.某人从观览车的最低处(地面A处)乘车,问经过4分钟后,此人距地面CD的高度是多少米?(观览车距最低处地面高度不计).
如图,石景山游乐园的观览车半径为25m,已知观览车绕圆心O顺时针做匀速运动,旋转一周用12分钟.某人从观览车的最低处(地面A处)乘车,问经过4分钟后,此人距地面CD的高度是多少米?(观览车距最低处地面高度不计).
解:连接OA,由题意得OA⊥CD,
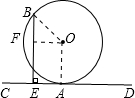
设旋转4分钟后,此人到达B处,连接OB,则∠AOB=360°× =120°,
=120°,
过B、O分别作BE⊥CD于E,OF⊥BE于F;
∴∠BFO=90°,
∴四边形OFEA为矩形,
∴FE=OA=25,∠BOF=120°-90°=30°;
在Rt△BFO中,
∵OB=25,
∴BF= OB=
OB= ,
,
∴BE=BF+FE= +25=37.5,
+25=37.5,
∴人距地面37.5m.
分析:连接OA,由题意得OA⊥CD.设旋转4分钟后,此人到达B处,连接OB,由旋转一周用12分钟;可知经过4分钟后,∠AOB=120°,过B、O分别作BE⊥CD于E,OF⊥BE于F,可知四边形OFEA为矩形;∠BOF=120°-90°=30°,根据直角三角形的性质可知,BF= OB,再根据切线的性质可求出答案.
OB,再根据切线的性质可求出答案.
点评:本题考查的是弧,弦,圆心角的关系及直角三角形的性质,解答此题的关键是根据题意画出图形,利用数形结合解答.

设旋转4分钟后,此人到达B处,连接OB,则∠AOB=360°×
 =120°,
=120°,过B、O分别作BE⊥CD于E,OF⊥BE于F;
∴∠BFO=90°,
∴四边形OFEA为矩形,
∴FE=OA=25,∠BOF=120°-90°=30°;
在Rt△BFO中,
∵OB=25,
∴BF=
 OB=
OB= ,
,∴BE=BF+FE=
 +25=37.5,
+25=37.5,∴人距地面37.5m.
分析:连接OA,由题意得OA⊥CD.设旋转4分钟后,此人到达B处,连接OB,由旋转一周用12分钟;可知经过4分钟后,∠AOB=120°,过B、O分别作BE⊥CD于E,OF⊥BE于F,可知四边形OFEA为矩形;∠BOF=120°-90°=30°,根据直角三角形的性质可知,BF=
 OB,再根据切线的性质可求出答案.
OB,再根据切线的性质可求出答案.点评:本题考查的是弧,弦,圆心角的关系及直角三角形的性质,解答此题的关键是根据题意画出图形,利用数形结合解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
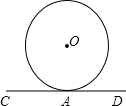 如图,石景山游乐园的观览车半径为25m,已知观览车绕圆心O顺时针做匀速运动,旋转一周用12分钟.某人从观览车的最低处(地面A处)乘车,问经过4分钟后,此人距地面CD的高度是多少米?(观览车距最低处地面高度不计).
如图,石景山游乐园的观览车半径为25m,已知观览车绕圆心O顺时针做匀速运动,旋转一周用12分钟.某人从观览车的最低处(地面A处)乘车,问经过4分钟后,此人距地面CD的高度是多少米?(观览车距最低处地面高度不计).