题目内容
在△ABC中,AB=AC=3,BC=2,则S△ABC等于( )
| A.3 | B.2 | C.2
| D.3
|
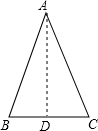
AB=AC=3,BC=2,作AD⊥BC,则AD为BC边上的高,
∵AB=AC,
∴D为BC边上的中点.
∴AD=
=2
,
∴S△ABC=
×BC×AD=2
.
故选 C.
∵AB=AC,
∴D为BC边上的中点.
∴AD=
| AB2-BD2 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
故选 C.


练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目




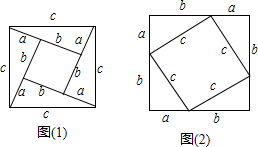 数学中一个十分著名的定理,这个定理结论的数学表达式是______.
数学中一个十分著名的定理,这个定理结论的数学表达式是______.