题目内容
(2012•萝岗区一模)在矩形AOBC中,OB=6,OA=4.分别以OB,OA所在直线为x轴和y轴,建立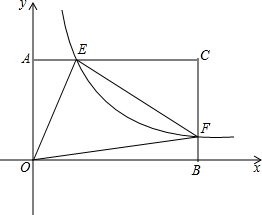 如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=
如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=
(k>0)的图象与AC边交于点E.
(1)设点E,F的坐标分别为:E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,求证:S1=S2;
(2)若y2=1,求△OEF的面积;
(3)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
 如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=
如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=| k | x |
(1)设点E,F的坐标分别为:E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,求证:S1=S2;
(2)若y2=1,求△OEF的面积;
(3)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
分析:(1)分别用点E,F的坐标表示出△AOE与△FOB的面积,再利用反比例函数的性质xy=k,再进行比较即可;
(2)根据题意可得E,F两点坐标分别为E(
,4),F(6,
),再利用y2=1,得出E,F坐标,进而求出△OEF的面积;
(3)应分别用矩形面积和能用图中的点表示出的三角形的面积表示出所求的面积,利用二次函数求出最值即可.
(2)根据题意可得E,F两点坐标分别为E(
| k |
| 4 |
| k |
| 6 |
(3)应分别用矩形面积和能用图中的点表示出的三角形的面积表示出所求的面积,利用二次函数求出最值即可.
解答: (1)证明:设E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,
(1)证明:设E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,
由题意得y1=
,y2=
,
∴S1=
x1y1=
k,S2=
x2y2=
k,
∴S1=S2;
(2)解:由题意知E,F两点坐标分别为E(
,4),F(6,
),
∵y2=1,∴
=1,
∴k=6,
∴E点坐标为:(
,4),F点坐标为:(6,1),
∴EC=6-
=
,FC=4-1=3,
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF,
=4×6-
×
×4-
×6×1-
×
×3,
=
;
(3)解:∵E,F两点坐标分别为E(
,4),F(6,
),
∴S△ECF=
EC•CF=
(6-
)(4-
),
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF,
=24-
k-
k-S△ECF,
=24-k-S△ECF,
∴S=S△OEF-S△ECF=24-k-2S△ECF=24-k-(24-2k+
k2),
=-
k2+k,
=-
(k-12)2+6,
当k=12时,S有最大值.
S最大值=6.
 (1)证明:设E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,
(1)证明:设E(x1,y1),F(x2,y2),△AOE与△FOB的面积分别为S1,S2,由题意得y1=
| k |
| x1 |
| k |
| x2 |
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S1=S2;
(2)解:由题意知E,F两点坐标分别为E(
| k |
| 4 |
| k |
| 6 |
∵y2=1,∴
| k |
| 6 |
∴k=6,
∴E点坐标为:(
| 3 |
| 2 |
∴EC=6-
| 3 |
| 2 |
| 9 |
| 2 |
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF,
=4×6-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
=
| 45 |
| 4 |
(3)解:∵E,F两点坐标分别为E(
| k |
| 4 |
| k |
| 6 |
∴S△ECF=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 4 |
| k |
| 6 |
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF,
=24-
| 1 |
| 2 |
| 1 |
| 2 |
=24-k-S△ECF,
∴S=S△OEF-S△ECF=24-k-2S△ECF=24-k-(24-2k+
| 1 |
| 24 |
=-
| 1 |
| 24 |
=-
| 1 |
| 24 |
当k=12时,S有最大值.
S最大值=6.
点评:此题主要考查了反比例函数的图象和性质、图形的面积计算、二次函数最值等知识,求坐标系内一般三角形的面积,通常整理为矩形面积减去若干直角三角形的面积的形式求出是解题关键.

练习册系列答案
相关题目
 (2012•萝岗区一模)如图,一次函数y=kx+b(k<0)的图象经过点A.当y>3时,x的取值范围是
(2012•萝岗区一模)如图,一次函数y=kx+b(k<0)的图象经过点A.当y>3时,x的取值范围是