题目内容
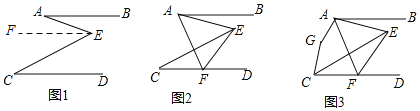
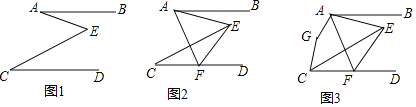
【题目】已知:AB∥CD,平面内有一点E,连接AE、CE
(1)如图1,求证:∠E=∠A+∠C;
(2)如图2,CD上有一点F,连接AF、EF,若∠FAE=∠FEA,∠EFD=2∠C,求证:∠AFC=2∠AEC;
(3)如图3,在(2)的条件下,平面内有一点G,连接AG、CG,若∠GCE与∠GAE互为补角,5∠AFC=2∠G,求∠G的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠G的度数为150°.
【解析】
(1)过E作EF∥AB,根据平行线的性质,即可得出∠A=∠AEF,∠C=∠CEF,进而得到∠AEC=∠AEF+∠CEF=∠A+∠C;
(2)设∠BAE=α,∠DCE=β,由(1)可得,∠AEC=∠BAE+∠C=α+β,根据角的和差关系可得,∠BAF=∠EAF+∠BAE=α+2β+α=2(α+β),最后根据∠AFC=∠BAF=2(α+β),可得∠AFC=2∠AEC;
(3)设∠G=α,根据5∠AFC=2∠G,可得∠AFC=![]() α,再根据∠AFC=2∠AEC,可得∠AEC=
α,再根据∠AFC=2∠AEC,可得∠AEC=![]() ∠AFC=
∠AFC=![]() α,最后根据四边形AECG中,∠GCE与∠GAE互为补角,可得∠G+∠AEC=180°,据此可得方程α+
α,最后根据四边形AECG中,∠GCE与∠GAE互为补角,可得∠G+∠AEC=180°,据此可得方程α+![]() α=180°,求得∠G的度数为150°.
α=180°,求得∠G的度数为150°.
(1)如图,过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠A+∠C;
(2)设∠BAE=α,∠DCE=β,则
由(1)可得,∠AEC=∠BAE+∠C=α+β,
∵∠EFD=2∠C,∠EFD=∠C+∠CEF,
∴∠C=∠CEF=β,
∴∠AEF=α+2β,
又∵∠FAE=∠FEA,
∴∠FAE=α+2β,
∴∠BAF=∠EAF+∠BAE=α+2β+α=2(α+β),
又∵AB∥CD,
∴∠AFC=∠BAF=2(α+β),
∴∠AFC=2∠AEC;
(3)设∠G=α,
根据5∠AFC=2∠G,可得∠AFC=![]() α,
α,
又∵∠AFC=2∠AEC,
∴∠AEC=![]() ∠AFC=
∠AFC=![]() α,
α,
∵四边形AECG中,∠GCE与∠GAE互为补角,
∴∠G+∠AEC=180°,
即α+![]() α=180°,
α=180°,
∴α=150°,
即∠G的度数为150°.