题目内容
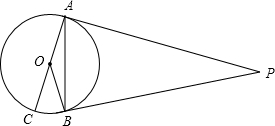 如图所示,PA,PB是⊙O的切线,AC是⊙O的直径,∠P=40°,则∠BAC=
如图所示,PA,PB是⊙O的切线,AC是⊙O的直径,∠P=40°,则∠BAC=分析:连接OP,根据切线的性质可求出△ADP≌△BPD及∠APD的度数,根据直角三角形的性质可求出∠DAP的度数,由切线的性质定理解答即可.
解答: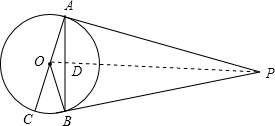 解:连接OP,根据切线的性质可知,
解:连接OP,根据切线的性质可知,
AP=BP,∠DAP=∠DPB=
∠P=
×40°=20°,
在△ADP与△BPD中,AP=BP,DP=DP,∠DAP=∠DPB=20°,
∴△ADP≌△BPD,OP⊥AB,
∴∠DAP=90°-∠DAP=90°-20°=70°,
∵AP是⊙O的切线,AC是直径,
∴∠OAP=90°,
∴∠BAC=∠OAP-∠DAP=90°-70°=20°.
 解:连接OP,根据切线的性质可知,
解:连接OP,根据切线的性质可知,AP=BP,∠DAP=∠DPB=
| 1 |
| 2 |
| 1 |
| 2 |
在△ADP与△BPD中,AP=BP,DP=DP,∠DAP=∠DPB=20°,
∴△ADP≌△BPD,OP⊥AB,
∴∠DAP=90°-∠DAP=90°-20°=70°,
∵AP是⊙O的切线,AC是直径,
∴∠OAP=90°,
∴∠BAC=∠OAP-∠DAP=90°-70°=20°.
点评:此题比较简单,解答此题的关键是连接OP,根据切线的性质定理解答.

练习册系列答案
相关题目
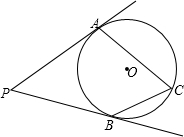 如图所示,PA、PB切⊙O于点A、B,∠P=70°,则∠ACB=( )
如图所示,PA、PB切⊙O于点A、B,∠P=70°,则∠ACB=( )| A、15° | B、40° | C、75° | D、55° |
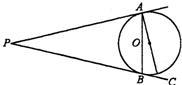
 18、如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.
18、如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=80°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数. 19、如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.
19、如图所示,PA、PB是⊙O的切线,A、B为切点,∠APB=40°,点C是⊙O上不同于A、B的任意一点,求∠ACB的度数.