题目内容
若正比例函数y=k1x(k1≠0)和反比例函数y=
(k2≠0)的图象的一个交点为(m、n),则另一个交点为
| k2 | x |
(-m,-n)
(-m,-n)
.分析:反比例函数的图象是中心对称图形,则经过原点的直线的两个交点一定关于原点对称.
解答:解:∵正比例函数y=k1x(k1≠0)和反比例函数y=
(k2≠0)的图象的两个交点关于原点对称,且一个交点为(m、n),
∴另一交点的坐标为(-m,-n).
故答案是:(-m,-n).
| k2 |
| x |
∴另一交点的坐标为(-m,-n).
故答案是:(-m,-n).
点评:本题主要考查了反比例函数图象的中心对称性,要求同学们要熟练掌握.

练习册系列答案
相关题目
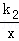 (k2≠0)的图象的一个交点为(m、n),则另一个交点为 .
(k2≠0)的图象的一个交点为(m、n),则另一个交点为 .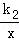 (k2≠0)的图象的一个交点为(m、n),则另一个交点为 .
(k2≠0)的图象的一个交点为(m、n),则另一个交点为 .