题目内容
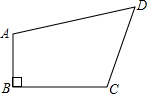 如图,在一块四边形ABCD空地中植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要元投入.
如图,在一块四边形ABCD空地中植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要元投入.
- A.16800
- B.7200
- C.5100
- D.无法确定
B
分析:连接AC,可得△ABC与△DAC均为直角三角形,进而可求解四边形的面积.
解答: 解:连接AC,
解:连接AC,
因为AB=3m,BC=4m,DA=13m,CD=12m,∠B=90°,
所以AC2=AB2+BC2 ,
=42+32,
=16+9,
=25,
所以AC=5m,
又因AD2-DC2,
=132-122,
=169-144,
=25,
=AC2,
所以△DAC为直角三角形,
因此S四边形ABCD的面积=S△ABC+S△DAC,
=AB×BC+AD×AC,
= ×4×3+
×4×3+ ×12×5,
×12×5,
=6+30,
=36.
故费用为:200×36=7200元,
故选B.
点评:本题考查了勾股定理及勾股定理的逆定理的应用,会用勾股定理逆定理求三角形是直角三角形.
分析:连接AC,可得△ABC与△DAC均为直角三角形,进而可求解四边形的面积.
解答:
 解:连接AC,
解:连接AC,因为AB=3m,BC=4m,DA=13m,CD=12m,∠B=90°,
所以AC2=AB2+BC2 ,
=42+32,
=16+9,
=25,
所以AC=5m,
又因AD2-DC2,
=132-122,
=169-144,
=25,
=AC2,
所以△DAC为直角三角形,
因此S四边形ABCD的面积=S△ABC+S△DAC,
=AB×BC+AD×AC,
=
 ×4×3+
×4×3+ ×12×5,
×12×5,=6+30,
=36.
故费用为:200×36=7200元,
故选B.
点评:本题考查了勾股定理及勾股定理的逆定理的应用,会用勾股定理逆定理求三角形是直角三角形.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
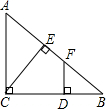 如图,在一块三角形绿地上开辟一块四边形花圃(四边形CDFE),AC=CB=10米,四边形花圃的最长边CD=8米,则三角形BDF的面积是
如图,在一块三角形绿地上开辟一块四边形花圃(四边形CDFE),AC=CB=10米,四边形花圃的最长边CD=8米,则三角形BDF的面积是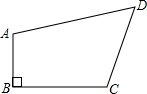 如图,在一块四边形ABCD空地中植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要( )元投入.
如图,在一块四边形ABCD空地中植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要( )元投入. 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是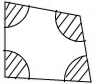 如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).
如图,在一块四边形场地的四个角修建四个半径为2米的扇花台,那么四个花台的总面积是________平方米(结果中保留π).