题目内容
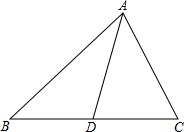 如图,AD为△ABC的中线,若△ABC的面积为40,AB=8,则D点到AB边的距离为
如图,AD为△ABC的中线,若△ABC的面积为40,AB=8,则D点到AB边的距离为5
5
.分析:根据三角形的中线把三角形分成两个面积相等的三角形求出△ABD的面积,再根据是三角形的面积公式列式计算即可得解.
解答:解:∵AD为△ABC的中线,
∴S△ABD=
S△ABC=
×40=20,
设D点到AB边的距离h,
则S△ABD=
AB•h=
×8h=20,
解得h=5.
故答案为:5.
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
设D点到AB边的距离h,
则S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
解得h=5.
故答案为:5.
点评:本题考查了三角形的面积,点到直线的距离,熟记三角形的中线把三角形分成两个面积相等的三角形求出△ABD的面积是解题的关键.

练习册系列答案
相关题目
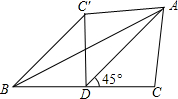 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.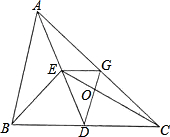 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.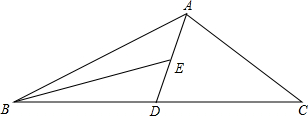 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.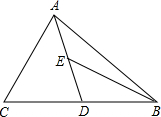 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.