题目内容
【题目】如图，数轴上有 A、B 两点，所表示的有理数分别为 a、b，已知 AB=12，原点 O 是线段AB 上的一点，且 OA=2OB.
（1）求a，b；
（2）若动点 P，Q 分别从 A，B 同时出发，向右运动，点 P 的速度为每秒 2 个单位长度，点 Q 的速度为每秒 1 个单位长度，设运动时间为 t 秒，当点 P 与点 Q 重合时，P，Q 两点停止运动.
①当 t 为何值时，2OPOQ=4；
②当点 P 到达点 O 时，动点 M 从点 O 出发，以每秒 3 个单位长度的速度也向右运动，当点 M 追上点 Q 后立即返回，以同样的速度向点 P 运动，遇到点 P 后再立即返回，以同样的速度向点 Q 运动，如此往返，直到点 P，Q 停止时，点 M 也停止运动，求在此过程中点 M 行驶的总路程，并直接写出点 M 最后位置在数轴上所对应的有理数.
【答案】（1）a=－8，b=4；（2）①当 t 为 1.6 秒或 8 秒时，2OP－OQ=4；②点 M 行驶的总路程为 24 和点 M 最后位置在数轴上对应的实数为16．
【解析】
（1）由AO=2OB可知，将12平均分成三份，AO占两份为8，OB占一份为4，由图可知，A在原点的左边，B在原点的右边，从而得出结论；
（2）①分两种情况：点P在原点的左侧和右侧时，OP表示的代数式不同，OQ=4+t，分别代入2OP﹣OQ=4列式即可求出t的值；
②点M运动的时间就是点P从点O开始到追到点Q的时间，设点M运动的时间为t秒，列式为t（2﹣1）=8，解出即可解决问题．
（1）∵AB=12，AO=2OB，∴AO=8，OB=4，∴A点所表示的实数为﹣8，B点所表示的实数为4，∴a=﹣8，b=4．
故答案为：﹣8；4；
（2）①当0＜t≤4时，如图3，AP=2t，OP=8﹣2t，BQ=t，OQ=4+t．
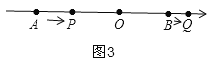
∵2OP﹣OQ=4，∴2（8﹣2t）﹣（4+t）=4，t=
=1.6；
当点P与点Q重合时，如图4，2t=12+t，t=12；
当4＜t＜12时，如图5，OP=2t﹣8，OQ=4+t，则2（2t﹣8）﹣（4+t）=4，t=8．
综上所述：当t为1.6秒或8秒时，2OP﹣OQ=4；
②当点P到达点O时，8÷2=4，此时，OQ=4+t=8，即点Q所表示的实数为8，如图6，设点M运动的时间为t秒，由题意得：2t﹣t=8，t=8，此时，点P表示的实数为8×2=16，所以点M表示的实数也是16，∴点M行驶的总路程为：3×8=24．
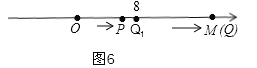
答：点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16．
【题目】近几年某市加大中职教育投入力度，取得了良好的社会效果．某校随机调查了九年级m名学生的升学意向，并根据调查结果绘制出不完整的统计表如下：
升学意向 | 省级示范高中 | 市级示范高中 | 一般高中 | 职业高中 | 其他 | 合计 |
人数 | 15 | 15 | 9 | 3 | m | |
百分比 | 25% | 25% | n | 5% | 100% |
请你根据统计表提供的信息解答下列问题：
（1）表中m的值为 ，n的值为 ；
（2）补全图7中的条形统计图；
（3）若该校九年级有学生500名，估计该校大约有多少名毕业生的升学意向是职业高中？
