题目内容
已知正六边形的周长为24cm,一圆与它各边都相切,则这个六边形的面积为( )
A、12
| ||
B、24
| ||
C、48
| ||
D、96
|
分析:连接OA、OB、ON,得到等边三角形AOB,求出AB、OA、OB,求出AN、NB,根据勾股定理求出ON,根据三角形面积公式求出即可.
解答: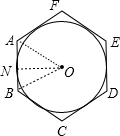 解:圆O与它各边都相切,
解:圆O与它各边都相切,
连接OA、OB、ON,
∠AOB=60°,OA=OB,
∴三角形AOB是等边三角形,
∴∠OBA=60°,
OA=AB=OB=
×24cm=4cm,
∴BN=AN=2cm,
由勾股定理得:ON=
=2
(cm),
∴正六边形的面积是6×
×2
cm×4cm=24
cm2.
故选B.
 解:圆O与它各边都相切,
解:圆O与它各边都相切,连接OA、OB、ON,
∠AOB=60°,OA=OB,
∴三角形AOB是等边三角形,
∴∠OBA=60°,
OA=AB=OB=
| 1 |
| 6 |
∴BN=AN=2cm,
由勾股定理得:ON=
| OB2-BN2 |
| 3 |
∴正六边形的面积是6×
| 1 |
| 2 |
| 3 |
| 3 |
故选B.
点评:本题主要考查对正多边形和圆,等腰三角形的性质,等边三角形的性质和判定,三角形的面积等知识点的理解和掌握,能求出ON的长是解此题的关键.

练习册系列答案
相关题目
 cm2
cm2