题目内容
在同一平面直角坐标系中,若一个反比例函数的图象与一次函数y=-2x+6的图象无公共点,则这个反比例函数的表达式是 (只写出符合条件的一个即可).
【答案】分析:两个函数在同一直角坐标系中的图象无公共点,其k要满足-2x2+6x-k=0,△<0即可.
解答:解:设反比例函数的解析式为:y=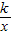 ,
,
∵一次函数y=-2x+6与反比例函数y=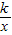 图象无公共点,则
图象无公共点,则 ,
,
∴-2x2+6x-k=0,
即△=62-8k<0
解得k> ,
,
则这个反比例函数的表达式可以是y=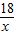 ;
;
故答案可为:y=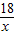 .
.
点评:此题考查了反比例函数与一次函数的交点问题.解题的关键是:两个函数在同一直角坐标系中的图象无公共点,其k要满足-2x2-6x-k=0的△<0.
解答:解:设反比例函数的解析式为:y=
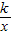 ,
,∵一次函数y=-2x+6与反比例函数y=
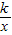 图象无公共点,则
图象无公共点,则 ,
,∴-2x2+6x-k=0,
即△=62-8k<0
解得k>
 ,
,则这个反比例函数的表达式可以是y=
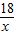 ;
;故答案可为:y=
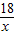 .
.点评:此题考查了反比例函数与一次函数的交点问题.解题的关键是:两个函数在同一直角坐标系中的图象无公共点,其k要满足-2x2-6x-k=0的△<0.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目


 直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )
直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )