题目内容
 如图,已知在△ABC中,BD、CE为高,D、E为垂足,连接DE.求证:∠ADE=∠ABC.
如图,已知在△ABC中,BD、CE为高,D、E为垂足,连接DE.求证:∠ADE=∠ABC.
证明:∵BD、CE是高,
∴∠ADB=∠AEC=90°.
又∵∠A=∠A,
∴△AEC∽△ADB,
∴ ,
,
即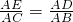 ,
,
∵∠EAD=∠CAB,
∴△AED∽△ACB,
∴∠ADE=∠ABC.
分析:由BD、CE是高,∠A是公共角,即可证得:△AEC∽△ADB,得到 ,又由对应边成比例且夹角相等的三角形相似,证得:△AED∽△ACB,则问题得证.
,又由对应边成比例且夹角相等的三角形相似,证得:△AED∽△ACB,则问题得证.
点评:此题考查了相似三角形的判定与性质.注意有两角对应相等的三角形相似与对应边成比例且夹角相等的三角形相似定理的应用.
∴∠ADB=∠AEC=90°.
又∵∠A=∠A,
∴△AEC∽△ADB,
∴
 ,
,即
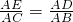 ,
,∵∠EAD=∠CAB,
∴△AED∽△ACB,
∴∠ADE=∠ABC.
分析:由BD、CE是高,∠A是公共角,即可证得:△AEC∽△ADB,得到
 ,又由对应边成比例且夹角相等的三角形相似,证得:△AED∽△ACB,则问题得证.
,又由对应边成比例且夹角相等的三角形相似,证得:△AED∽△ACB,则问题得证.点评:此题考查了相似三角形的判定与性质.注意有两角对应相等的三角形相似与对应边成比例且夹角相等的三角形相似定理的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
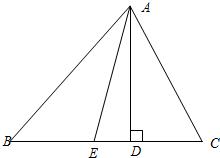
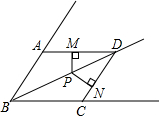 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.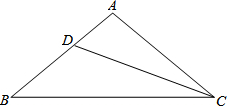 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.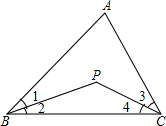 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为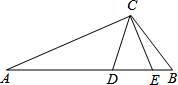 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.