题目内容
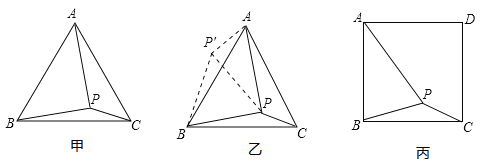
【题目】问题：如图甲，在等边三角形
内有一点
，且
，
，
，求
度数的大小和等边三角形
的边长
探究：解题思路是：将
绕点
逆时针旋转
，如图乙，连接
（1）
是_______三角形，
是______三角形，
（2）利用
可以求出
的边长为_______
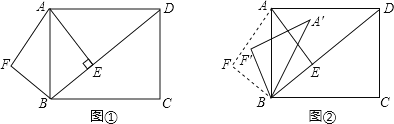
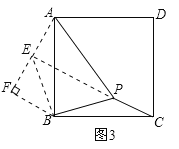
拓展应用：如图丙，在正方形
内有一点
，且
，
，
（3）求
度数的大小
（4）求正方形
的边长
【答案】（1）等边；直角；
；（2）
；（3）
；（4）
【解析】
试题分析：
探究：将
绕点
顺时针旋转
，画出旋转后的图形（如图2），连接
，可得
是等边三角形，而
又是直角三角形（由勾股定理的逆定理可证），所以
，而
，进而求出等边
的边长为
，问题得到解决
拓展应用：求出
，根据勾股定理的逆定理求出
，推出
，过点
作
，交
延长线于点
，求出
，
，利用勾股定理即可求出
试题解析：
解：（1）∵
是等边三角形
∴
将
绕点
顺时针旋转
得出
∴
，
，
，
∵
∴
∴
是等边三角形
∴
，
∵
，
∴
∴
，则
是直角三角形
∴
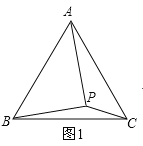
（2）过点
作
，交
的延长线于点
∴
，
由勾股定理得：
故答案为：等边；直角；；
（3）将
绕点
逆时针旋转
得到
与（1）类似：可得
，
，
，
∴
∴
由勾股定理得：
∵
，
，
∴
∴
∴
（4）过点
作
，交
的延长线于点
∴
∴
∴
∴在
中，由勾股定理，得
∴
，正方形边长为
练习册系列答案
相关题目
