题目内容
 (2012•金牛区二模)如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O的直经BD=6,连接CD、AO、BC,且AO与BC相交于点E.
(2012•金牛区二模)如图,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O的直经BD=6,连接CD、AO、BC,且AO与BC相交于点E.(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)请阅读下方资源链接内容.在(2)的基础上,若CD、AO的长分别为一元二次方程x2-(4m+1)x+4m2+2=0的两个实数根,求AB的长.
分析:(1)连接OC,由AB与AC都为圆的切线,根据切线的性质AC垂直于OC,AB与OB垂直,根据垂直的定义得到两个角为直角,在直角三角形ACO与直角三角形ABO中,由OC=OB,OA为公共边,利用HL得出三角形ACO与三角形ABO全等,根据全等三角形的对应边及对应角相等得到AB=AC,∠1=∠2,根据三线合一得到AO与BC垂直,又BD为圆O的直径,根据直径所对的圆周角为直角,得到CD与BC垂直,可得出DC与AO都与BC垂直,则AO平行于CD,得证;
(2)由第一问得到CD与AO平行,根据两直线平行同位角相等可得出∠3=∠4,再由一对直角相等,利用两对对应角相等的两三角形相似,可得出三角形BDC与三角形ABO相似,根据相似得比例,将各自的边长代入即可得出y与x的关系式,并根据直径为6,圆中的弦长小于等于直径可得出x的取值范围;
(3)由CD、AO的长分别为一元二次方程x2-(4m+1)x+4m2+2=0的两个实数根,根据根与系数的关系表示出xy,根据第二问得出的y与x的关系式得到xy=18,列出关于m的方程,求出方程的解得到m的值,将m的值代入原方程,求出方程的解,可得出CD及AO的值,由CD=OB得出OB的长,在直角三角形ABO中,由AO及OB的长,利用勾股定理即可求出AB的长.
(2)由第一问得到CD与AO平行,根据两直线平行同位角相等可得出∠3=∠4,再由一对直角相等,利用两对对应角相等的两三角形相似,可得出三角形BDC与三角形ABO相似,根据相似得比例,将各自的边长代入即可得出y与x的关系式,并根据直径为6,圆中的弦长小于等于直径可得出x的取值范围;
(3)由CD、AO的长分别为一元二次方程x2-(4m+1)x+4m2+2=0的两个实数根,根据根与系数的关系表示出xy,根据第二问得出的y与x的关系式得到xy=18,列出关于m的方程,求出方程的解得到m的值,将m的值代入原方程,求出方程的解,可得出CD及AO的值,由CD=OB得出OB的长,在直角三角形ABO中,由AO及OB的长,利用勾股定理即可求出AB的长.
解答: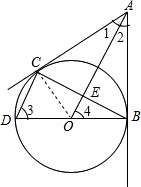 解:(1)连接OC,…(1分)
解:(1)连接OC,…(1分)
∵AB、AC是⊙O的切线,
∴∠ACO=∠ABO=90°,
在Rt△ACO和Rt△ABO中,
,
∴Rt△ACO≌Rt△ABO(HL),
∴AB=AC,∠1=∠2,
∴AO⊥BC,
∴∠AEC=90°,…(2分)
∵BD是⊙O的直径,∴∠DCB=90°,
∴∠DCB=∠AEC,
∴CD∥AO;…(3分)
(2)∵CD∥AO,∴∠3=∠4,
∵AB是⊙O的切线,DB是直径,
∴∠DCB=∠ABO=90°,
∴△BDC∽△AOB,…(4分)
∴
=
,即
=
,
∴y=
,…(5分)
且自变量x的取值范围为0<x<6;…(6分)
(3)∵CD、AO的长分别为一元二次方程x2-(4m+1)x+4m2+2=0的两个实数根,
∴x•y=4m2+2,…(7分)
又由(2)知y=
,
∴xy=18,
∴4m2+2=18,
∴m=±2,…(8分)
①当m=2时,原方程可化为x2-9x+18=0,∴x=3或6;
由(2)知x<6,∴只能取x=3,
∴CD=3,AO=6,
在Rt△AOB中,AO=6,OB=3,
∴AB=
=3
;…(9分)
②当m=-2时,原方程可化为x2+7x+18=0,
∵△=72-4×1÷18<0,∴方程无解,…(10分)
综上,AB的长为3
.
 解:(1)连接OC,…(1分)
解:(1)连接OC,…(1分)∵AB、AC是⊙O的切线,
∴∠ACO=∠ABO=90°,
在Rt△ACO和Rt△ABO中,
|
∴Rt△ACO≌Rt△ABO(HL),
∴AB=AC,∠1=∠2,
∴AO⊥BC,
∴∠AEC=90°,…(2分)
∵BD是⊙O的直径,∴∠DCB=90°,
∴∠DCB=∠AEC,
∴CD∥AO;…(3分)
(2)∵CD∥AO,∴∠3=∠4,
∵AB是⊙O的切线,DB是直径,
∴∠DCB=∠ABO=90°,
∴△BDC∽△AOB,…(4分)
∴
| BD |
| AO |
| DC |
| OB |
| 6 |
| y |
| x |
| 3 |
∴y=
| 18 |
| x |
且自变量x的取值范围为0<x<6;…(6分)
(3)∵CD、AO的长分别为一元二次方程x2-(4m+1)x+4m2+2=0的两个实数根,
∴x•y=4m2+2,…(7分)
又由(2)知y=
| 18 |
| x |
∴xy=18,
∴4m2+2=18,
∴m=±2,…(8分)
①当m=2时,原方程可化为x2-9x+18=0,∴x=3或6;
由(2)知x<6,∴只能取x=3,
∴CD=3,AO=6,
在Rt△AOB中,AO=6,OB=3,
∴AB=
| 62-33 |
| 3 |
②当m=-2时,原方程可化为x2+7x+18=0,
∵△=72-4×1÷18<0,∴方程无解,…(10分)
综上,AB的长为3
| 3 |
点评:此题考查了切线的性质,圆周角定理,等腰三角形的性质,平行线的判定,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,以及根与系数的关系,是一道综合性较强的题,要求学生掌握知识要全面.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 (2012•金牛区二模)阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为
(2012•金牛区二模)阅读材料:C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.设CD=x,若AB=4,DE=2,BD=8,则可用含x的代数式表示AC+CE的长为