��Ŀ����
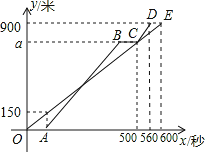
����Ŀ���ס������˴����깬����������ͬ��·�ֱ��Բ�ͬ���ٶ�����������������������һ��·�̺����ҿ�ʼ���������ҳ�����150��ʱ����ͣ�ڴ˵صȺ�����������������ּ�����ԭ�����ٶ���������������ͼ�Ǽס����������ܲ���ȫ�����о�����·��y��������׳�����ʱ��x�������ĺ���ͼ����
��1�����ܲ���ȫ�������������� ���� ���ٶ�Ϊ ��/�룻
��2�����ܲ����ٶ��Ƕ��٣�����;�еȺ�����˶ʱ�䣿
��3���׳����ʱ���һ��������������ʱ�����˶����ף�
���𰸡���1��900��1��5��/�룻��2��100������3���׳���250����ҵ�һ����������ʱ������375����
��������
�����������1���յ�E�����������·�������������ʱ�䣻
��2���������C����õĺ���������a��ֵ����CD�ε�·�̿��������ʱ����560-500=60���������ܲ����ٶȼ�����ã�
B��ʱ�����õ�ʱ����������Ȼ�����·����150��ʱ�����õ�ʱ���������ҳ�����ʱ�������ߵIJ��������
��3��������ü��˶��ĺ����Լ�AB�εĺ�����������������Ľ������꼴����
�����������1������ͼ����Եõ���������900��������600�������ٶ�����900��600=1��5��/�룻
��2������500��ʱ��·������500��1��5=750������CD�εij���900-750=150����ʱ������560-500=60�������ٶ�����150��60=2��5��/�룻
����150���õ�ʱ������150��1��5=100������ױ��������100����
����750���õ�ʱ������750��2��5=300����������;�еȺ���õ�ʱ������500-300-100=100����
��3����ÿ����1��5�������·����ʱ��ĺ�����ϵʽ����y=1��5x��
������100������ÿ����2��5������AB�εĺ�������ʽ����y=2��5��x-100����
�����������1��5x=2��5��x-100���������x=250����
�ҵ�·������2��5����250-100��=375��������
�����׳���250����ҵ�һ����������ʱ������375����