题目内容
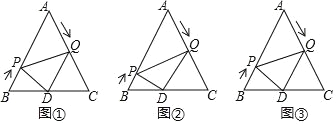
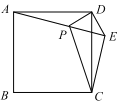
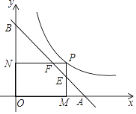
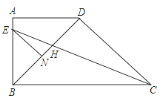
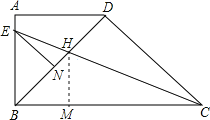
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD⊥DC,BD=DC,CE平分∠BCD,交AB于点E,交BD于点H,EN∥DC交BD于点N.下列结论:
①BH=DH;②CH=(![]() +1)EH;③
+1)EH;③![]() =
=![]() . 其中正确的是( )
. 其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①②③
【答案】B
【解析】
①如图,过H作HM⊥BC于M,根据角平分线的性质可以得到DH=HM,而在Rt△BHM中BH>HM,所以容易判定①是错误的;
②设HM=x,那么DH=x,由于∠ABC=90°,BD⊥DC,BD=DC,由此得到∠DBC=45°,而AD∥CB,由此可以证明△ADB是等腰直角三角形,又CE平分∠BCD,∠BDC=∠ABC=90°,由此可以证明△DCH∽△EBC,再利用相似三角形的性质可以推出∠BEH=∠DHC,然后利用对顶角相等即可证明∠BHC=∠BEH,接着得到BH=BE,然后即可用x分别表示BE、EN、CD,又由EN∥DC可以得到△DCH∽△NEH,再利用相似三角形的性质即可结论②;
③利用(2)的结论可以证明△ENH∽△CBE,然后利用相似三角形的性质和三角形的面积公式即可证明结论③.
①如图,过H作HM⊥BC于M,
∵CE平分∠BCD,BD⊥DC
∴DH=HM,
而在Rt△BHM中BH>HM,
∴BH>HD,
∴所以容易判定①是错误的;
②∵CE平分∠BCD,
∴∠DCE=∠BCE,而∠EBC=∠BDC=90°,
∴∠BEH=∠DHC,
而∠DHC=∠EHB,
∴∠BEH=∠EHB,
∴BE=BH,
设HM=x,那么DH=x,
∵BD⊥DC,BD=DC,
∴∠DBC=∠ABD=45°,
∴BH=![]() x=BE,
x=BE,
∴EN=x,
∴CD=BD=DH+BH=(![]() +1)x,
+1)x,
即![]() ,
,
∵EN∥DC,
∴△DCH∽△NEH,
∴![]() ,即CH=(
,即CH=(![]() +1)EH;
+1)EH;
③由②得∠BEH=∠EHB,
∵EN∥DC,
∴∠ENH=∠CDB=90°,
∴∠ENH=∠EBC,
∴△ENH∽△CBE,
∴EH:EC=NH:BE,
而![]() ,
,
∴![]() .
.
所以正确的只有②③.
故选B.

【题目】我校为了迎接体育中考,了解学生的体育成绩,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制作图如下:
成绩段 | 频数 | 频率 |
160≤x<170 | 5 | 0.1 |
170≤x<180 | 10 | a |
180≤x<190 | b | 0.14 |
190≤x<200 | 16 | c |
200≤x<210 | 12 | 0.24 |
表(1)
根据图表解决下列问题:
(1)本次共抽取了多少名学生进行体育测试,表(1)中,a、b、c分别等于多少?
(2)补全图(2),所抽取学生成绩中中位数在哪个分数段;
(3)“跳绳”数在180以上,则此项成绩可得满分.那么,你估计全校九年级有多少学生在此项成绩中获满分?
【题目】八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知:A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).