题目内容
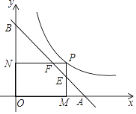
【题目】如图,P为反比例函数y= ![]() (x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=﹣x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AFBE的值为________.
(x>0)图象上一点,过点P分别向x轴,y轴作垂线,垂足分别为M、N,直线y=﹣x+2与PM、PN分别交于点E、F,与x轴、y轴分别交于A、B,则AFBE的值为________.
【答案】3
【解析】
如图,过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,由直线y=-x+2与x轴、y轴分别交于A、B,可得△AOB是等腰直角三角形,继而可得△AFH也是等腰直角三角形,△BGE为等腰直角三角形,从而可得AF=![]() PM,BE=
PM,BE=![]() PN,可得AF×BE =2PMPN,由点P在y=
PN,可得AF×BE =2PMPN,由点P在y=![]() 上,可得PMPN=
上,可得PMPN=![]() ,继而可求得AF×BE=2PMPN=3,问题得以解决.
,继而可求得AF×BE=2PMPN=3,问题得以解决.
如图,过F点作FH⊥x轴于H,过E点作EG⊥y轴于G,则有FH=PM,PN=EG,
∵直线y=-x+2与x轴、y轴分别交于A、B,
∴A(2,0),B(0,2),
∴△AOB是等腰直角三角形,
∴△AFH也是等腰直角三角形,△BGE为等腰直角三角形,
∴AH=FH,BG=EG,
∴AF=![]() =
=![]() FH=
FH=![]() PM,BE=
PM,BE=![]() =
=![]() EG=
EG=![]() PN,
PN,
∴AF×BE=![]() PM×
PM×![]() PN=2PMPN,
PN=2PMPN,
∵y=![]() ,
,
∴PMPN=![]() ,
,
∴AF×BE=2PMPN=2×![]() =3,
=3,
故答案为:3.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目