题目内容
19、如图,线段AB上有两点C,D,且点D是线段CB的中点,AC=3,CD=5,则图中所有线段长的和是
44
.
分析:首先求出图中有六条不同的线段,然后分别求出它们的长,最后将它们相加即可.
解答:解:图中的线段有:AC,AD,AB,CD,CB,DB.
∵点D是线段CB的中点,CD=5,
∴DB=CD=5,CB=2CD=10,
又∵AC=3,
∴AD=AC+CD=8,
AB=AC+CB=13.
∴AC+AD+AB+CD+CB+DB=3+8+13+5+10+5=44.
∵点D是线段CB的中点,CD=5,
∴DB=CD=5,CB=2CD=10,
又∵AC=3,
∴AD=AC+CD=8,
AB=AC+CB=13.
∴AC+AD+AB+CD+CB+DB=3+8+13+5+10+5=44.
点评:本题关键是求出图中有多少条不同的线段.
如果一条直线上有n个点,那么这条直线上有$frac{n(n-1)}{2}$条线段,本题n=4.
如果一条直线上有n个点,那么这条直线上有$frac{n(n-1)}{2}$条线段,本题n=4.

练习册系列答案
相关题目
 如图,线段AB上有两点P,Q,点P将AB分成两部分.AP=
如图,线段AB上有两点P,Q,点P将AB分成两部分.AP=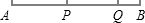 如图,线段AB上有两点P,Q,点P将AB分成两部分.AP=
如图,线段AB上有两点P,Q,点P将AB分成两部分.AP= PB,点Q将AB也分成两部分,AQ=4QB,PQ=3cm,求AP、QB的长.
PB,点Q将AB也分成两部分,AQ=4QB,PQ=3cm,求AP、QB的长.