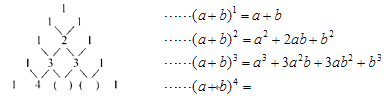ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚ
Έ“Ο«÷ΣΒάΘ§ΥΡ±Ώ–ΈΨΏ”–≤ΜΈ»Ε®–‘Θ§»ί“Ή±δ–ΈΘ§»γΆΦ1Θ§“ΜΗωΨΊ–ΈΖΔ…ζ±δ–ΈΚσ≥…ΈΣ“ΜΗωΤΫ––ΥΡ±Ώ–ΈΘ§…η’βΗωΤΫ––ΥΡ±Ώ–ΈœύΝΎΝΫΗωΡΎΫ«÷–Ϋœ–ΓΒΡ“ΜΗωΡΎΫ«ΈΣΠΝΘ§Έ“Ο«Α―![]() ΒΡ÷ΒΫ–Ήω’βΗωΤΫ––ΥΡ±Ώ–ΈΒΡ±δ–ΈΕ»Θ°
ΒΡ÷ΒΫ–Ήω’βΗωΤΫ––ΥΡ±Ώ–ΈΒΡ±δ–ΈΕ»Θ°
Θ®1Θ©»τΨΊ–ΈΖΔ…ζ±δ–ΈΚσΒΡΤΫ––ΥΡ±Ώ–Έ”–“ΜΗωΡΎΫ« «120Ε»Θ§‘ρ’βΗωΤΫ––ΥΡ±Ώ–ΈΒΡ±δ–ΈΕ» « Θ°
≤¬œκ÷ΛΟςΘΚ
Θ®2Θ©…ηΨΊ–ΈΒΡΟφΜΐΈΣS1Θ§Τδ±δ–ΈΚσΒΡΤΫ––ΥΡ±Ώ–ΈΟφΜΐΈΣS2Θ§ ‘≤¬œκS1Θ§S2Θ§![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΆΊ’ΙΧΫΨΩΘΚ
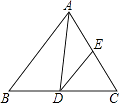
Θ®3Θ©»γΆΦ2Θ§‘ΎΨΊ–ΈABCD÷–Θ§E «AD±Ώ…œΒΡ“ΜΒψΘ§«“![]() =AEADΘ§’βΗωΨΊ–ΈΖΔ…ζ±δ–ΈΚσΈΣΤΫ––ΥΡ±Ώ–ΈA1B1C1D1Θ§E1ΈΣEΒΡΕ‘”ΠΒψΘ§Ν§Ϋ”B1E1Θ§B1D1Θ§»τΨΊ–ΈABCDΒΡΟφΜΐΈΣ
=AEADΘ§’βΗωΨΊ–ΈΖΔ…ζ±δ–ΈΚσΈΣΤΫ––ΥΡ±Ώ–ΈA1B1C1D1Θ§E1ΈΣEΒΡΕ‘”ΠΒψΘ§Ν§Ϋ”B1E1Θ§B1D1Θ§»τΨΊ–ΈABCDΒΡΟφΜΐΈΣ![]() Θ®mΘΨ0Θ©Θ§ΤΫ––ΥΡ±Ώ–ΈA1B1C1D1ΒΡΟφΜΐΈΣ
Θ®mΘΨ0Θ©Θ§ΤΫ––ΥΡ±Ώ–ΈA1B1C1D1ΒΡΟφΜΐΈΣ![]() Θ®mΘΨ0Θ©Θ§ ‘«σΓœA1E1B1+ΓœA1D1B1ΒΡΕ» ΐΘ°
Θ®mΘΨ0Θ©Θ§ ‘«σΓœA1E1B1+ΓœA1D1B1ΒΡΕ» ΐΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©30ΓψΘ°
ΘΜΘ®3Θ©30ΓψΘ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΒΟΒΫΠΝ=60ΓψΘ§ΗυΨί»ΐΫ«Κ· ΐΒΡΕ®“εΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©»γΆΦ1Θ§…ηΨΊ–ΈΒΡ≥ΛΚΆΩμΖ÷±πΈΣaΘ§bΘ§±δ–ΈΚσΒΡΤΫ––ΥΡ±Ώ–ΈΒΡΗΏΈΣhΘ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΚΆΨΊ–ΈΒΡΟφΜΐΙΪ ΫΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®3Θ©”…“―÷ΣΧθΦΰΒΟΒΫΓςB1A1E1ΓΉΓςD1A1B1Θ§”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœA1B1E1=ΓœA1D1B1Θ§ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟΒΫΓœA1E1B1=ΓœC1B1E1Θ§«σΒΟΓœA1E1B1+ΓœA1D1B1=ΓœC1E1B1+ΓœA1B1E1=ΓœA1B1C1Θ§÷ΛΒΟΓœA1B1C1=30ΓψΘ§”Ύ «ΒΟΒΫΫα¬έΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏΤΫ––ΥΡ±Ώ–Έ”–“ΜΗωΡΎΫ« «120Ε»Θ§ΓύΠΝ=60ΓψΘ§Γύ![]() =
=![]() =
=![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©![]() Θ§άμ”…ΘΚ»γΆΦ1Θ§…ηΨΊ–ΈΒΡ≥ΛΚΆΩμΖ÷±πΈΣaΘ§bΘ§±δ–ΈΚσΒΡΤΫ––ΥΡ±Ώ–ΈΒΡΗΏΈΣhΘ§ΓύS1=abΘ§S2=ahΘ§sinΠΝ=
Θ§άμ”…ΘΚ»γΆΦ1Θ§…ηΨΊ–ΈΒΡ≥ΛΚΆΩμΖ÷±πΈΣaΘ§bΘ§±δ–ΈΚσΒΡΤΫ––ΥΡ±Ώ–ΈΒΡΗΏΈΣhΘ§ΓύS1=abΘ§S2=ahΘ§sinΠΝ=![]() Θ§Γύ
Θ§Γύ![]() =
=![]() =
=![]() Θ§ΓΏ
Θ§ΓΏ![]() =
=![]() Θ§Γύ
Θ§Γύ![]() ΘΜ
ΘΜ
Θ®3Θ©ΓΏ![]() =AEADΘ§Γύ
=AEADΘ§Γύ![]() =A1E1A1D1Θ§Φ¥
=A1E1A1D1Θ§Φ¥![]() Θ§ΓΏΓœB1A1E1=ΓœD1A1B1Θ§ΓύΓςB1A1E1ΓΉΓςD1A1B1Θ§ΓύΓœA1B1E1=ΓœA1D1B1Θ§ΓΏA1D1ΓΈB1C1Θ§ΓύΓœA1E1B1=ΓœC1B1E1Θ§ΓύΓœA1E1B1+ΓœA1D1B1=ΓœC1E1B1+ΓœA1B1E1=ΓœA1B1C1Θ§”…Θ®2Θ©÷Σ
Θ§ΓΏΓœB1A1E1=ΓœD1A1B1Θ§ΓύΓςB1A1E1ΓΉΓςD1A1B1Θ§ΓύΓœA1B1E1=ΓœA1D1B1Θ§ΓΏA1D1ΓΈB1C1Θ§ΓύΓœA1E1B1=ΓœC1B1E1Θ§ΓύΓœA1E1B1+ΓœA1D1B1=ΓœC1E1B1+ΓœA1B1E1=ΓœA1B1C1Θ§”…Θ®2Θ©÷Σ![]() Θ§Ω…÷Σ
Θ§Ω…÷Σ![]() =
=![]() =2Θ§ΓύsinΓœA1B1C1=
=2Θ§ΓύsinΓœA1B1C1=![]() Θ§ΓύΓœA1B1C1=30ΓψΘ§ΓύΓœA1E1B1+ΓœA1D1B1=30ΓψΘ°
Θ§ΓύΓœA1B1C1=30ΓψΘ§ΓύΓœA1E1B1+ΓœA1D1B1=30ΓψΘ°