题目内容
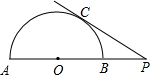已知：如图，AB是半圆O的直径，P是AB延长线上的一点，若OB=BP，则∠P的度数为（ ）| A、60° | B、45° | C、30° | D、15° |
分析：连接OC，由切线的性质易知△OCP是Rt△，已知OB=BP=OC，即∠P所对的边是斜边的一半，根据直角三角形的性质即可得到∠P的度数．
解答：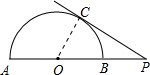
解：连接OC；
∵PC切⊙O于C，
∴OC⊥PC，
Rt△OCP中，OC=OB=BP，即OC=
OP；
所以∠P=30°，故选C．
解：连接OC；∵PC切⊙O于C，
∴OC⊥PC，
Rt△OCP中，OC=OB=BP，即OC=
| 1 |
| 2 |
所以∠P=30°，故选C．
点评：此题主要考查的是直角三角形及切线的性质．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
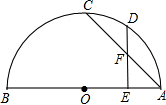已知：如图，AB为⊙O的直径，C、D是半圆弧上的两点，E是AB上除O外的一点，AC与DE相交于F．①
=-
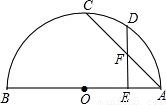
，②DE⊥AB，③AF=DF．
，②DE⊥AB，③AF=DF．
，②DE⊥AB，③AF=DF．