题目内容
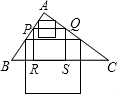
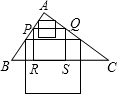
如图,已知锐角△ABC的边BC的长为6,面积为12,PQ∥BC,点P在AB上,点Q在AC上,四边形RPQS为正方形(RS与A在PQ的异侧),其边长为x,正方形RPQS与△ABC的公共面积为y.
(1)当正方形RPQS的边RS恰好落在BC上时,求边长x.
(2)当RS不落在BC上时,求y关于x的函数关系式以及自变量x的取值范围.(可以将图形画在备用的图形中)
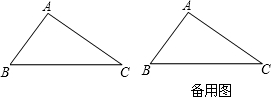
(3)求y的最大值.
解:(1)设△ABC的高为h,
∵△ABC的边BC的长为6,面积为12,
∴ ×h×BC=12,
×h×BC=12,
∴h=4,
则△APQ的高=h-x=4-x,
∵PQ∥BC,四边形RPQS为正方形(RS与A在PQ的异侧),
∴△APQ∽△ABC,
∴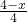 =
=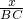 ,即
,即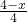 =
=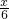 ,
,
解得x=2.4.
答;当正方形RPQS的边RS恰好落在BC上时,边长x为2.4;
(2)中RS不落在BC上意味着RS可以落在三角形的内部或外部两种情形.
①当RS落在三角形内时,如图(1),
y=x2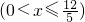
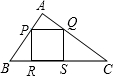
当RS落在三角形外时,如图(2),
过A作AE⊥BC于E交PQ于D,
同上 设PQ=x,则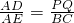 ,
,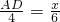 ,
,
∴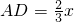 ,
,
∴DE= ,
,
∴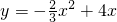
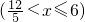 ;
;
(3)①当RS落在△ABC外部时,
 ,
,
∴当x=3时,y有最大值是6;
②当RS落在BC边上时,由x= 可知,y=
可知,y=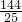 ,
,
③当RS落在△ABC内部时,y=x2(0<x< )
)
故比较以上三种情况可知,公共部分面积最大为6.
分析:(1)当RS落在BC上时,先求△ABC的BC边上的高,由△APQ∽△ABC,利用对应高的比等于相似比即可求出x;
(2)分为当RS落在△ABC的外部和内部两种情况,当RS在△ABC的外部时,由相似得公共部分的长、宽表示面积,当RS在△ABC的内部时,正方形面积即为公共部分面积;
(3)根据(1)(2)所求函数关系式,结合自变量取值范围分别求最大值,比较得出结论.
点评:本题考查了二次函数在求长方形面积中的应用,解答此题的关键是根据题意表示长方形的面积,再根据自变量的取值范围及二次函数的最值求法求解,本题还考查了分类讨论的教学思想.总之,这是一道非常典型的题目.
∵△ABC的边BC的长为6,面积为12,
∴
 ×h×BC=12,
×h×BC=12,∴h=4,
则△APQ的高=h-x=4-x,
∵PQ∥BC,四边形RPQS为正方形(RS与A在PQ的异侧),
∴△APQ∽△ABC,
∴
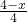 =
=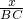 ,即
,即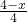 =
=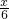 ,
,解得x=2.4.

答;当正方形RPQS的边RS恰好落在BC上时,边长x为2.4;
(2)中RS不落在BC上意味着RS可以落在三角形的内部或外部两种情形.
①当RS落在三角形内时,如图(1),
y=x2
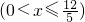
当RS落在三角形外时,如图(2),

过A作AE⊥BC于E交PQ于D,
同上 设PQ=x,则
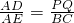 ,
,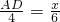 ,
,∴
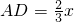 ,
,∴DE=
 ,
,∴
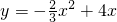
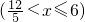 ;
;(3)①当RS落在△ABC外部时,
 ,
,∴当x=3时,y有最大值是6;
②当RS落在BC边上时,由x=
 可知,y=
可知,y=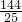 ,
,③当RS落在△ABC内部时,y=x2(0<x<
 )
)故比较以上三种情况可知,公共部分面积最大为6.
分析:(1)当RS落在BC上时,先求△ABC的BC边上的高,由△APQ∽△ABC,利用对应高的比等于相似比即可求出x;
(2)分为当RS落在△ABC的外部和内部两种情况,当RS在△ABC的外部时,由相似得公共部分的长、宽表示面积,当RS在△ABC的内部时,正方形面积即为公共部分面积;
(3)根据(1)(2)所求函数关系式,结合自变量取值范围分别求最大值,比较得出结论.
点评:本题考查了二次函数在求长方形面积中的应用,解答此题的关键是根据题意表示长方形的面积,再根据自变量的取值范围及二次函数的最值求法求解,本题还考查了分类讨论的教学思想.总之,这是一道非常典型的题目.

练习册系列答案
相关题目
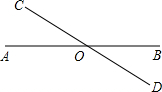 如图,已知直线AB和CD相交于点O(∠AOC为锐角)
如图,已知直线AB和CD相交于点O(∠AOC为锐角) 如图,已知直线AB和CD相交于点O(∠AOC为锐角)
如图,已知直线AB和CD相交于点O(∠AOC为锐角)