题目内容
已知在△AOB中,∠B=90°,AB=OB,点O的坐标为(0,0),点A的坐标为(0,4),点B在第一象限内,将这个三角形绕原点O逆时针旋转75°后,那么旋转后点B的坐标为 .
【答案】分析:易得△AOB的等腰直角三角形,那么OB的长为2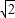 ,绕原点O逆时针旋转75°后,那么点B与y轴正半轴组成30°的角,利用相应的三角函数可求得旋转后点B的坐标.
,绕原点O逆时针旋转75°后,那么点B与y轴正半轴组成30°的角,利用相应的三角函数可求得旋转后点B的坐标.
解答:解:∵∠B=90°,AB=OB,点O的坐标为(0,0),点A的坐标为(0,4),
∴OA=4.
∴OB=2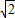 ,
,
∵将这个三角形绕原点O逆时针旋转75°,
∴点B与y轴正半轴组成30°的角,
点B的横坐标为-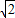 ,纵坐标为
,纵坐标为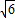 .
.
∴旋转后点B的坐标为(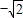 ,
,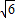 ).
).
点评:解决本题的关键是利用旋转的性质得到旋转后与点B的坐标相关的角度和线段的长度.
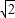 ,绕原点O逆时针旋转75°后,那么点B与y轴正半轴组成30°的角,利用相应的三角函数可求得旋转后点B的坐标.
,绕原点O逆时针旋转75°后,那么点B与y轴正半轴组成30°的角,利用相应的三角函数可求得旋转后点B的坐标.解答:解:∵∠B=90°,AB=OB,点O的坐标为(0,0),点A的坐标为(0,4),
∴OA=4.
∴OB=2
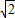 ,
,∵将这个三角形绕原点O逆时针旋转75°,
∴点B与y轴正半轴组成30°的角,
点B的横坐标为-
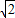 ,纵坐标为
,纵坐标为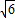 .
.∴旋转后点B的坐标为(
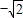 ,
,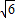 ).
).点评:解决本题的关键是利用旋转的性质得到旋转后与点B的坐标相关的角度和线段的长度.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目