题目内容
已知在△AOB中,∠B=90°,AB=OB,点O的坐标为(0,0),点A的坐标为(0,8),点B在第一象限内,将这个三角形绕原点O旋转75°后,那么旋转后点B的坐标为 .
【答案】分析:先根据点A的坐标求出OA的长,再根据等腰直角三角形的性质求出OB的长,然后分①逆时针旋转时,过点B′作B′C′⊥y轴于C′,根据旋转角求出∠B′OC′=30°,然后求出B′C′、OC′的长,再写出旋转后点B的坐标即可;②顺时针旋转时,过点B″作B″C″⊥x轴于C″,根据旋转角求出∠B″OC″=30°,然后求出B″C″、OC″,然后写出旋转后点B对应的点的坐标即可.
解答: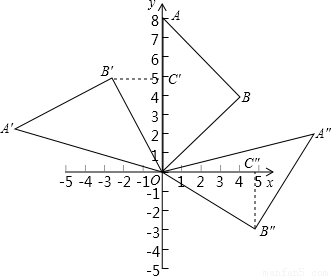 解:∵A(0,8),
解:∵A(0,8),
∴OA=8,
∵∠B=90°,AB=OB,
∴△AOB是等腰直角三角形,
∴OB=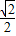 OA=
OA=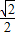 ×8=4
×8=4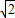 ,∠AOB=45°,
,∠AOB=45°,
①逆时针旋转时,过点B′作B′C′⊥y轴于C′,
∵旋转角为75°,
∴∠B′OC′=75°-45°=30°,
∴B′C′= OB′=
OB′= ×4
×4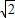 =2
=2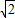 ,
,
OC′=4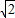 ×
×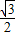 =2
=2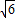 ,
,
∴旋转后点B的坐标为(-2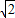 ,2
,2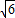 );
);
②顺时针旋转时,过点B″作B″C″⊥x轴于C″,
∵旋转角为75°,
∴∠B″OC″=75°-45°=30°,
∴B″C″= OB″=
OB″= ×4
×4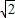 =2
=2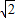 ,
,
OC″=4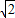 ×
×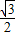 =2
=2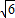 ,
,
∴旋转后点B的坐标为(2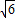 ,-2
,-2 );
);
综上所述,旋转后点B的坐标为(2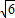 ,-2
,-2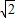 )或(-2
)或(-2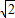 ,2
,2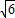 ).
).
点评:本题考查了坐标与图形变化-旋转,等腰直角三角形的性质,熟记旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键,难点在于要分情况讨论,作出图形更形象直观.
解答:
 解:∵A(0,8),
解:∵A(0,8),∴OA=8,
∵∠B=90°,AB=OB,
∴△AOB是等腰直角三角形,
∴OB=
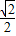 OA=
OA=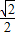 ×8=4
×8=4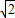 ,∠AOB=45°,
,∠AOB=45°,①逆时针旋转时,过点B′作B′C′⊥y轴于C′,
∵旋转角为75°,
∴∠B′OC′=75°-45°=30°,
∴B′C′=
 OB′=
OB′= ×4
×4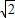 =2
=2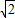 ,
,OC′=4
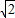 ×
×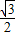 =2
=2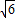 ,
,∴旋转后点B的坐标为(-2
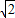 ,2
,2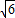 );
);②顺时针旋转时,过点B″作B″C″⊥x轴于C″,
∵旋转角为75°,
∴∠B″OC″=75°-45°=30°,
∴B″C″=
 OB″=
OB″= ×4
×4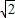 =2
=2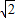 ,
,OC″=4
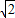 ×
×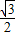 =2
=2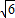 ,
,∴旋转后点B的坐标为(2
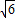 ,-2
,-2 );
);综上所述,旋转后点B的坐标为(2
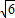 ,-2
,-2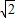 )或(-2
)或(-2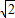 ,2
,2 ).
).点评:本题考查了坐标与图形变化-旋转,等腰直角三角形的性质,熟记旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键,难点在于要分情况讨论,作出图形更形象直观.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目