��Ŀ����
����Ŀ��һ���쳵�Ӽؿ����ҵأ�һ���������ҵؿ����أ�����ͬʱ���������������ҵ�Ϊy1��km�����쳵���ҵصľ���Ϊy2��km����������ʻʱ��Ϊx��h��������֮��ľ���Ϊs��km����y1 ��y2��x�ĺ�����ϵͼ����ͼ����ʾ��s��x�ĺ�����ϵͼ��ͼ����ʾ��
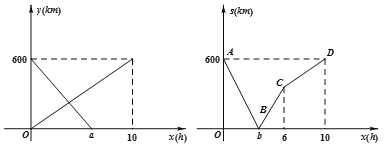
ͼ�� ͼ��
��1��ͼ�е�a= ��b= .
��2����s����x�ĺ�����ϵʽ.
��3���ס������ؼ���E��F��������վ�����200km���������������վEʱ���쳵ǡ�ý������վF����ֱ��д������վE���صľ���.
���𰸡���1��6�� ![]() ����2��
����2��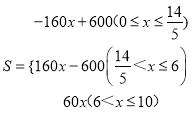 ����3������վE���صľ���Ϊ300ǧ��450ǧ��.
����3������վE���صľ���Ϊ300ǧ��450ǧ��.
����������1������S��x֮��ĺ�����ϵʽ���Եõ���λ��C��ʱ������֮��ľ������ӱ仺����ʱ�쳵��վ��ָ����ʱa��ֵ���ɣ����a��ֵ�������������ʱ��ʱ�伴Ϊb��ֵ��
��2�����ݺ�����ͼ����Եõ�A��B��C��D�ĵ�����꣬���ô���ϵ������ú����Ľ���ʽ���ɣ�
��3������������ǰ����������������������ۣ�������ǰ��s=200����ֱ��AB����ʽ������������s=200����ֱ��BC����ʽ�������x��ֵ��
�⣺(1)��S��x֮��ĺ�����ͼ���֪����λ��C��ʱ������֮��ľ������ӱ仺��
���ɴ˿��Եõ�a=6��
��쳵ÿСʱ��ʻ100ǧ�ף�����ÿСʱ��ʻ60ǧ�ף�����֮��ľ���Ϊ600��
��b=600��(100+60)= ![]() ��
��
(2)�ߴӺ�����ͼ���Ͽ��Եõ�A��B��C��D�������ֱ�Ϊ��(0,600)��(![]() ,0)��(6,360)��(10,600)��
,0)��(6,360)��(10,600)��
�����߶�AB����ֱ�߽���ʽΪ��S=kx+b��
��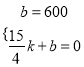 ��
��
��ã�k=160��b=600��
���߶�BC���ڵ�ֱ�ߵĽ���ʽΪ��S=kx+b��
��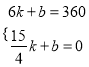
��ã�k=160��b=600��
��ֱ��CD�Ľ���ʽΪ��S=kx+b��
��![]() ��
��
��ã�k=60��b=0
��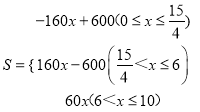 ��
��
(3)����������ǰ�ֱ����������ͬ�ļ���վ��
��ʱ��S=160x+600=200��
��ã�x=![]() ��
��
������������ֱ����������ͬ�ļ���վ��
��ʱ��S=160x600=200��
��ã�x=5��
�൱x=![]() ��5ʱ����ʱE����վ���صľ���Ϊ450km��300km.
��5ʱ����ʱE����վ���صľ���Ϊ450km��300km.