题目内容
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC、CD. 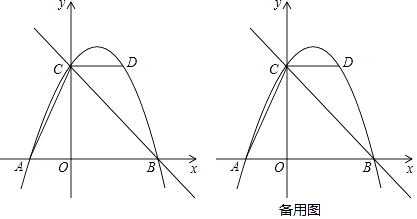
(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标.
【答案】
(1)解:∵抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),
∴设抛物线的解析式为y=a(x﹣x1)(x﹣x2),
∴y=a(x+2)(x﹣4),
∴﹣8a=4,
∴a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣ ![]() x2+x+4
x2+x+4
(2)解:①当点E在直线CD的抛物线上方,记E′,连接CE′,过点E′作E′F′⊥CD,垂足为F′,
由(1)得OC=4,
∵∠ACO=∠E′OF′,
∴tan∠ACO=tan∠E′CF′,
∴ ![]() =
= ![]() =
= ![]() ,
,
设线段E′F′=h,则CF′=2h,
∴点E′(2h,h+4),
∵点E′在抛物线上,
∴﹣ ![]() (2h)2+2h+4=h+4,
(2h)2+2h+4=h+4,
∴h1=0(舍去),h2= ![]() ,
,
∴E′(1, ![]() );
);
②当点E在直线CD的抛物线下方;
同①的方法得,E(3, ![]() ),
),
综上,点E的坐标为(1, ![]() ),(3,
),(3, ![]() ).
).
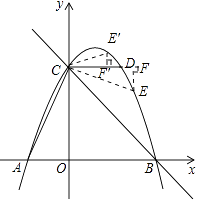
【解析】(1)设抛物线的解析式为y=a(x﹣x1)(x﹣x2),再把点代入即可得出解析式;(2)分两种情况:①当点E在直线CD的抛物线上方;②当点E在直线CD的抛物线下方;连接CE,过点E作EF⊥CD,再由三角函数得出点E的坐标.

练习册系列答案
相关题目