题目内容
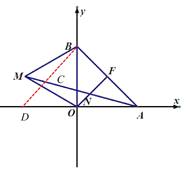
【题目】如图，在平面直角坐标系中，点A(n，0)是 x 轴上一点，点 B(0，m)是y轴上一点，且满足多项式(x＋m)(nx－2)的积中 x的二次项与一次项系数均为2.
（1）求出A,B两点坐标.
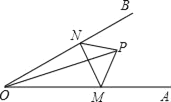
（2）如图1，点M为线段OA上一点，点P为 x 轴上一点，且满足BM＝MN，∠NAP=45°，证明：BM⊥MN.
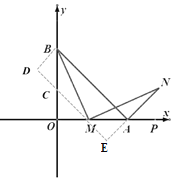
（3）如图2，过O作OF⊥AB于F，以OB为边在y轴左侧作等边△OBM，连接AM交OF于点N，试探究：在线段AF，AN，MN中，哪条线段等于AM与ON差的一半？请写出这个等量关系并证明.
【答案】（1）A（2，0），B（0，2）；（2）见解析；（3）AN=
(AM-ON)，证明见解析
【解析】
（1）计算(x＋m)(nx－2)，然后令二次项系数和一次项系数均为2求出m、n的值，即可得出A、B的坐标；
（2）在y轴上取一点使得OC=OM，过点B作BD⊥MC于点D，延长NA与CM交于点E，先证△BDC≌△AEM，再证△BDM≌△MEN，得到∠BMD=∠N，然后由直角三角形的两锐角互余等量代换即可得出结论；
（3）在AM上截取一点C使CM=ON，连接BC并延长交x轴于点D．由∠BOM=60°得∠MOD=30°，由等腰三角形的性质和三角形外角的性质可得∠OMA=∠OAM=15°，得到∠BAM=30°，∠BMA=45°，可证△OAN≌△BMC，可得到∠ABC=90°，进而利用含30°角直角三角形的性质和线段的和差关系即可得出结论．
（1）解：(x＋m)(nx－2)=nx2+(mn+2)x-2m，
∵x的二次项与一次项系数均为2，
∴
，
解得m=2，n=2，
∴A（2，0），B（0，2）；
（2）在y轴上取一点使得OC=OM，过点B作BD⊥MC于点D，延长NA与CM交于点E，
∵OC=OM，∠COM=90°，
∴∠OCM=∠OMC=45°，
∴∠DCB=∠OCM=45°，∠AME=∠OMC=45°，
∴∠DCB=∠AME，
∵∠MAE=∠NAP=45°，
在△BDC中，∠DBC=90°-45°=45°，
∴∠MAE=∠DBC，
∵OA=OB，OM=OC，
∴AM=BC，
在△BDC和△AEM中，
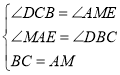
∴△BDC≌△AEM（AAS），
∴BD=AE，
∴BD=ME，
在Rt△BDM和Rt△MEN中，
，
∴△BDM≌△MEN（HL），
∴∠BMD=∠N，
∵∠N+∠NME=90°，
∴∠BMD+∠NME=90°，
∴∠BMN=90°，
∴BM⊥MN；
（3）（3）AN=(AM-ON)．
证明：在AM上截取一点C使CM=ON，连接BC并延长交x轴于点D．
∵△OBM是等边三角形，
∴∠BOM=∠BMO=60°，MB=OB=2，
∴∠MOD=90°-60°=30°，
∵OM=OA，
∴∠OMA=∠OAM=15°，
∵OA=OB，OB⊥OA，
∴∠OBA=∠OAB=45°，
∴∠BAM=45°-15°=30°，
∠BMA=60°-15°=45°，
∵△AOB是等腰直角三角形，OF⊥AB，
∴∠AON=45°，
∵OA=2，∴OA=MB，
在△OAN和△BMC中，
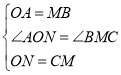
∴△OAN≌△BMC（SAS），
∴∠OAN=∠MBC=15°，AN=BC，
∴∠ABC=45°+60°-15°=90°，
在Rt△ABC中∠BAM=30°，
∴BC=AC，
∴AN=AC=(AM-CM)= (AM-ON)．
